Предел и непрерывность функции комплексного переменного
Пусть однозначная функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки  , исключая, может быть, саму точку
, исключая, может быть, саму точку  . Под
. Под 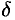 -окрестностью точки
-окрестностью точки  комплексной плоскости понимают внутренность круга радиуса
комплексной плоскости понимают внутренность круга радиуса 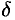 с центром в точке
с центром в точке  .
.
Число 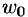 называется пределом функции
называется пределом функции  в точке
в точке  (или при
(или при 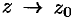 ), если для любого положительного
), если для любого положительного 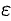 найдется такое положительное число
найдется такое положительное число 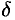 , что для всех
, что для всех 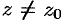 , удовлетворяющих неравенству
, удовлетворяющих неравенству 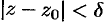 , выполняется неравенство
, выполняется неравенство 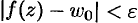 .
.
Записывают: 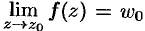 . Это определение коротко можно записать так:
. Это определение коротко можно записать так:
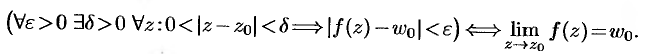
Из определения следует, что если предел 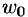 существует, то существуют и пределы
существует, то существуют и пределы
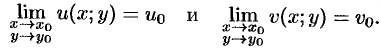
Верно и обратное утверждение.
Теоремы об арифметических свойствах пределов для функции одного (или нескольких) действительного переменного остаются справедливыми и для функции комплексного переменного. Так, если функции 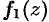 и
и 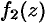 имеют пределы в точке
имеют пределы в точке 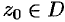 , то
, то
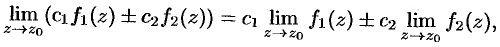
где 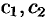 — постоянные;
— постоянные;
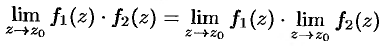
и
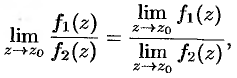
если 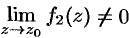 .
.
Пусть функция  определена в точке
определена в точке 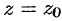 и в некоторой ее окрестности. Функция
и в некоторой ее окрестности. Функция  называется непрерывной в точке
называется непрерывной в точке  , если
, если 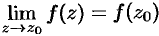 .
.
Определение непрерывности можно сформулировать и так: функция  непрерывна в точке
непрерывна в точке  , если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции:
, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции:
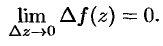
Функция  непрерывна в области
непрерывна в области  , если она непрерывна в каждой точке этой области.
, если она непрерывна в каждой точке этой области.
Модуль непрерывной функции комплексного переменного обладает теми же свойствами, что и непрерывная функция действительного переменного (см. теорема 43.1).
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Векторные дифференциальные операции первого порядка |
| Векторные дифференциальные операции второго порядка |
| Основные элементарные функции комплексного переменного |
| Ряды в комплексной плоскости |

