Оглавление:
Предел функции в точке
Пусть даны два непустых множества 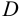 и
и 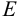 . Если каждому элементу
. Если каждому элементу 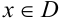 ставится в соответствие один и только одни элемент
ставится в соответствие один и только одни элемент 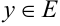 , то
, то 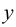 называется функцией
называется функцией 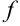 аргумента
аргумента 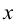 . Это записывается в виде:
. Это записывается в виде: 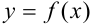
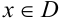 или
или 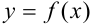 ,
, 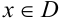 .
.
Пусть функция 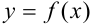 определена на некотором числовом множестве
определена на некотором числовом множестве 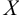 . Точка
. Точка 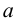 является предельной точкой этого множества, т. е. в любой малой окрестности точки
является предельной точкой этого множества, т. е. в любой малой окрестности точки 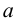 содержатся
содержатся 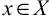 , отличные от
, отличные от 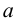
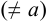 . Точка
. Точка 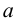 может принадлежать множеству
может принадлежать множеству 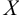 , а может и не принадлежать, т. е. функция может быть и не определена в точке
, а может и не принадлежать, т. е. функция может быть и не определена в точке 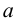 .
.
Функция  имеет предел
имеет предел 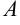 (конечный или бесконечный) при
(конечный или бесконечный) при 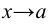 (в предельной точке
(в предельной точке 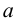 ), если для любой стремящейся к
), если для любой стремящейся к 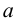 последовательности значений аргумента
последовательности значений аргумента 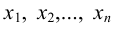 , входящей в область определения функции, но не равных а, соответствующая последовательность значений функции
, входящей в область определения функции, но не равных а, соответствующая последовательность значений функции 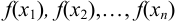 всегда стремится к
всегда стремится к 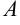 .
. 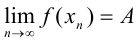 .
.
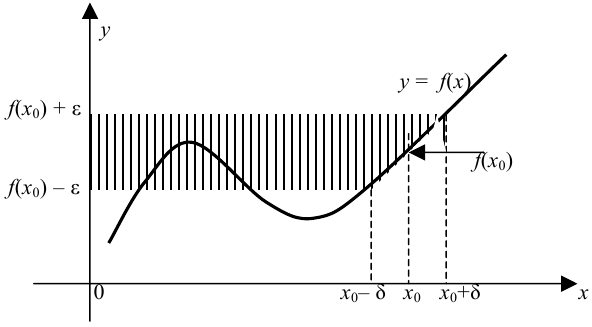
Число 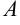 называется пределом функции
называется пределом функции 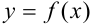 в точке
в точке 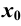 , если для любого сколь угодно малого
, если для любого сколь угодно малого 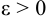 , существует такое
, существует такое 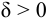 , что при всех
, что при всех 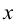 удовлетворяет условию
удовлетворяет условию 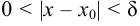 следует неравенство
следует неравенство 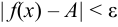 . Этот факт принято записывать так:
. Этот факт принято записывать так: 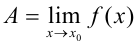 .
.
Свойства пределов
- Функция
 называется бесконечно малой при
называется бесконечно малой при 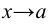 , если
, если 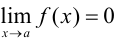 .
. - Функция
 называется бесконечно большой при
называется бесконечно большой при 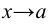 , если имеет место одно из равенств:
, если имеет место одно из равенств: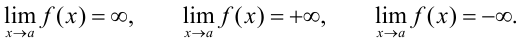
- Функция —
 бесконечно мала при
бесконечно мала при 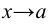 , если
, если  — мала.
— мала. - Если функции
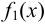 и
и 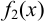 бесконечно малы при
бесконечно малы при 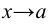 , то
, то 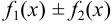 тоже бесконечно малы при
тоже бесконечно малы при 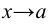 .
. - Если
 бесконечно мала, a
бесконечно мала, a 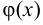 ограничена, то произведение
ограничена, то произведение 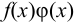 — бесконечно малая величина.
— бесконечно малая величина. - Если
 имеет конечный предел, а
имеет конечный предел, а 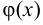 — бесконечно велика, то сумма их — бесконечно велика, т. е.
— бесконечно велика, то сумма их — бесконечно велика, т. е. 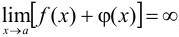 , а
, а 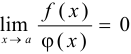 .
. - Если
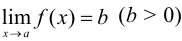 , a
, a 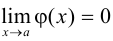 , причем
, причем 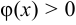 в окрестности точки
в окрестности точки 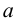 , то
, то 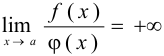 .
. - Произведение двух бесконечно больших функций есть функция бесконечно большая
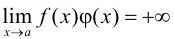 .
. - Если
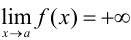 , то
, то 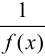 — бесконечно малая и
— бесконечно малая и 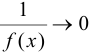 .
. - Если
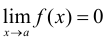 , то
, то 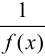 — бесконечно большая и
— бесконечно большая и 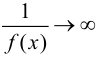 .
.
Правила предельного перехода
1. Если 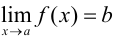 , а
, а 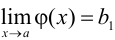 , то
, то 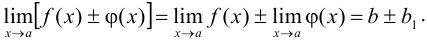
2. Если 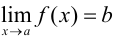 , и
, и 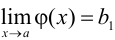 , то
, то 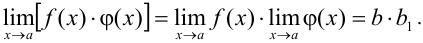
3. Если 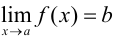 , а
, а 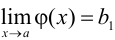 ,
, 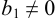 , то
, то 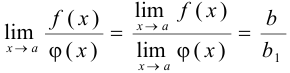 .
.
4. Предел целой рациональной функции.
Если 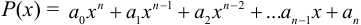 , то
, то 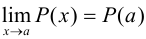 , т. е. при отыскании предела целой рациональной функции можно в выражении функции заменить аргумент его предельным значением. Если
, т. е. при отыскании предела целой рациональной функции можно в выражении функции заменить аргумент его предельным значением. Если
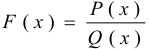 , то
, то
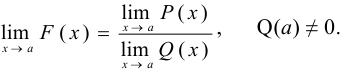
5. При постоянном показателе степени можно переходить к пределу в основании степени при условии, что предел основания степени существует, т. е. 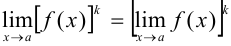 .
.
6. Если существует 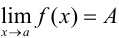 и
и 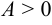 , то
, то
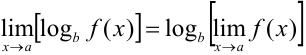
Задача №36.
Найти 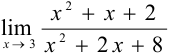 .
.
Решение:
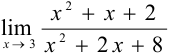
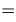 {подставим значение
{подставим значение 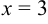 }
} 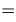
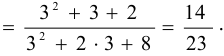
Задача №37.
Найти 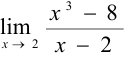 .
.
Решение:
При 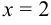 знаменатель равен 0. Следовательно, теорему о пределе дроби применить нельзя. Но так как
знаменатель равен 0. Следовательно, теорему о пределе дроби применить нельзя. Но так как 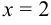 не входит в область определения функции и
не входит в область определения функции и 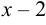
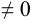 , то разделим числитель и знаменатель на
, то разделим числитель и знаменатель на 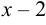 .
.
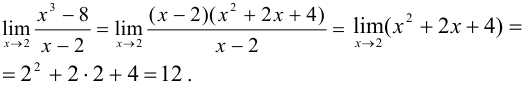
Правило. Для того, чтобы определить предел дробнорациональной функции в случае, когда 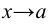 числитель и знаменатель дроби имеют пределы равные 0, надо числитель и знаменатель дроби разделить на
числитель и знаменатель дроби имеют пределы равные 0, надо числитель и знаменатель дроби разделить на 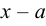 перейти к пределу. Если и после этого числитель и знаменатель равны 0, то надо повторить деление еще раз.
перейти к пределу. Если и после этого числитель и знаменатель равны 0, то надо повторить деление еще раз.
Задача №38.
Найти 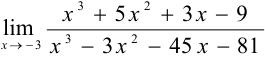 .
.
Решение:
Подставляя в данное выражение вместо 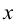 значение -3, имеем неопределенность
значение -3, имеем неопределенность 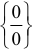 . Числитель и знаменатель дроби раз-делим на разность
. Числитель и знаменатель дроби раз-делим на разность 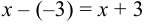 :
:
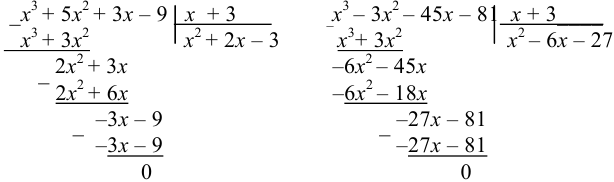
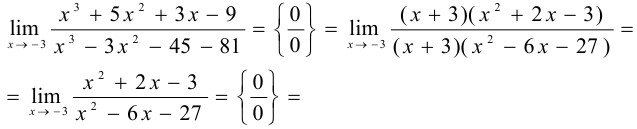
Делим еще раз числитель и знаменатель на 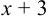 :
:
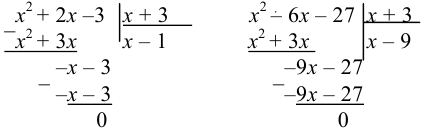
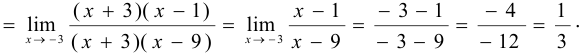
Задача №39.
Найти 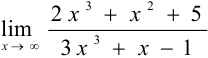 .
.
Решение:
Имеем неопределенность 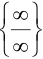 . Разделим числитель и знаменатель на наивысшую степень дроби
. Разделим числитель и знаменатель на наивысшую степень дроби 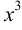 .
.
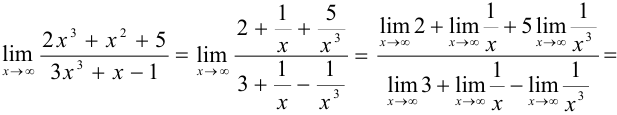
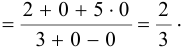
Задача №40.
Найти 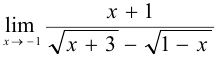 .
.
Решение:
Так как имеем неопределенность 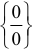 , то теорему о пределе частного применить нельзя. Данное выражение преобразуем, домножив числитель и знаменатель на выражение, сопряженное знаменателю, т. е. на
, то теорему о пределе частного применить нельзя. Данное выражение преобразуем, домножив числитель и знаменатель на выражение, сопряженное знаменателю, т. е. на 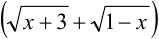 , получим
, получим
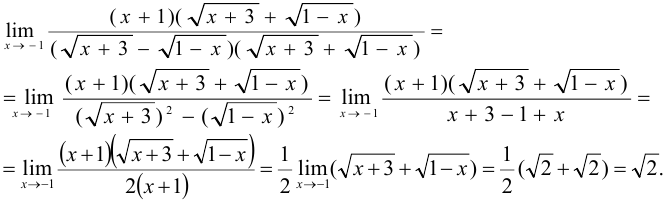
Правило. Чтобы найти предел дроби, содержащей иррациональные выражения в случае, когда предел и числителя и знаменателя дроби равен 0, надо перенести иррациональность из числителя в знаменатель или, наоборот, после этого сделать необходимые упрощения и перейти к пределу.
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
| Числовые последовательности задачи с решением |
| Предел числовой последовательности задачи с решением |
| Первый замечательный предел задача с решением |
| Второй замечательный предел задача с решением |

