Оглавление:
Предел функции в точке
Пусть функция 
определена в некоторой окрестности точки 
, кроме, быть может, самой точки .
Сформулируем два, эквивалентных между собой, определения предела функции в точке.
Определение 1 (на «языке последовательностей», или по Гейне). Число 
называется пределом функции в точке (или при 
), если для любой последовательности допустимых значений аргумента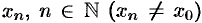 
, сходящейся к (т. е.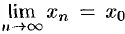 
), последовательность соответствующих значений функции 
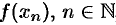, сходится к числу 
.
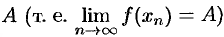В этом случае пишут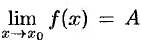 
или 
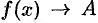при .
Геометрический смысл предела функции: 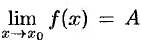означает, что для всех точек 
, достаточно близких к точке
, соответствующие значения функции как угодно мало отличаются от числа
.
Определение 2 (на «языке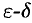 
», или по Коши). Число
называется пределом функции в точке
(или при ), если для любого положительного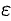 
найдется такое положительное число 
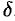, что для всех 
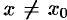, удовлетворяющих неравенству 
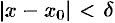, выполняется неравенство 
.
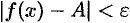Записывают 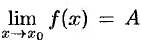. Это определение коротко можно записать так:
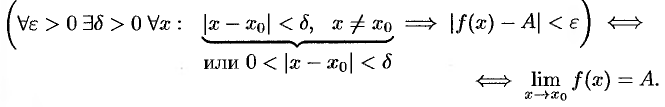
Геометрический смысл предела функции: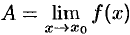 
, если для любой 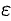-окрестности точки 
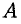найдется такая 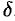-окрестность точки
, что для всех 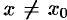из этой 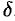-окрестности соответствующие значения функции 
лежат в 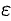-окрестности точки 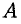. Иными словами, точки графика функции
лежат внутри полосы шириной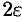 
, ограниченной прямыми 
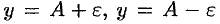(см. рис. 110). Очевидно, что величина 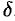зависит от выбора 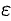, поэтому пишут 
.
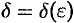Пример №16.1.
Доказать, что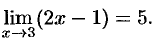 
Решение:
Возьмем произвольное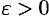 
, найдем 
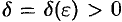такое, что для всех , удовлетворяющих неравенству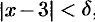 
, выполняется неравенство 
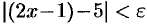, т. е. 
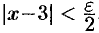. Взяв 
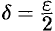, видим, что для всех , удовлетворяющих неравенству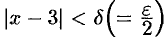 
, выполняется неравенство 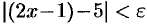. Следовательно,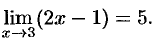
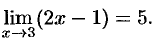
Дополнительный пример №16.2.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Уравнения плоскости в пространстве |
| Числовые последовательности |
| Односторонние пределы |
| Предел функции при х к бесконечности |
