Предел функции при х к бесконечности
Пусть функция  определена в промежутке
определена в промежутке 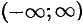 . Число
. Число  называется пределом функции
называется пределом функции  при
при 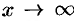 , если для любого положительного числа
, если для любого положительного числа 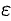 существует такое число
существует такое число 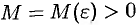 , что при всех
, что при всех  , удовлетворяющих неравенству
, удовлетворяющих неравенству  выполняется неравенство
выполняется неравенство 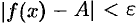 . Коротко это определение можно записать так:
. Коротко это определение можно записать так:
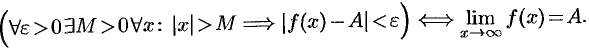
Если 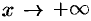 , то пишут
, то пишут 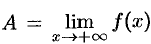 , если
, если 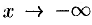 , то
, то 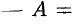
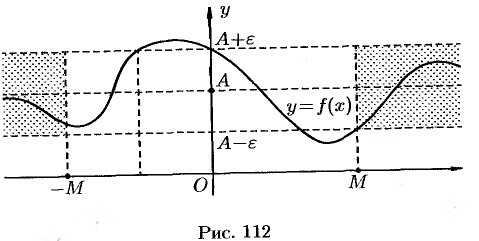
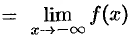 . Геометрический смысл этого определения таков: для
. Геометрический смысл этого определения таков: для  , что при
, что при 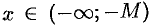 или
или 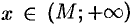 соответствующие значения функции
соответствующие значения функции  попадают в
попадают в 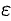 -окрестность точки
-окрестность точки  , т. е. точки графика лежат в полосе шириной 2
, т. е. точки графика лежат в полосе шириной 2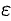 , ограничений прямыми
, ограничений прямыми 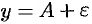 и
и 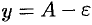 (см. рис. 112).
(см. рис. 112).
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Предел функции в точке |
| Односторонние пределы |
| Бесконечно большая функция |
| Бесконечно малые функции |

