Предел функции на бесконечности. Вычисление пределов путем раскрытии неопределенности вида 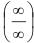 .
.
Число 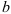 называется пределом функции
называется пределом функции 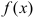 при
при  , если для любого наперед заданного
, если для любого наперед заданного 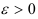 существует такое
существует такое 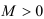 , что для всех
, что для всех 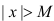 имеет место неравенство:
имеет место неравенство: 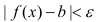 . Если
. Если 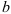 есть предел функции
есть предел функции 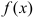 при
при  , то пишут:
, то пишут: 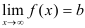 .
.
Для нахождения пределов функций на бесконечности часто используют два основных предела:
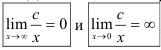
где  — константа.
— константа.
При вычислении предела дроби при  возникает неопределенность вида
возникает неопределенность вида 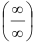 .Техника ее раскрытия заключается в том, что каждое слагаемое числителя и знаменателя нужно разделить на х в наивысшей степени. Возможны три случая:
.Техника ее раскрытия заключается в том, что каждое слагаемое числителя и знаменателя нужно разделить на х в наивысшей степени. Возможны три случая:
1 )наивысшая степень числителя совпадает с наивысшей степенью знаменателя:
Пример решения заказа контрольной работы №27.
Вычислитe
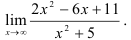
Решение:
Разделим каждое слагаемое числителя и знаменателя на 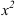 . Получим:
. Получим:
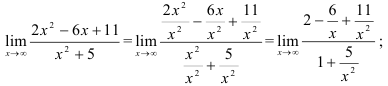
Каждое слагаемое 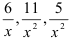 стремится к 0 при
стремится к 0 при  , тогда
, тогда
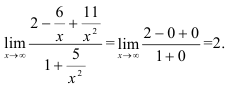
Ответ:
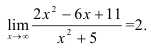
Итак, если наивысшая степень числителя совпадает с наивысшей степенью знаменателя, то в пределе получается число, отличное от нуля.
На этой странице вы сможете заказать контрольную работу и познакомиться с теорией и другими примерами решения:
Заказать контрольную работу по высшей математике
Другие похожие примеры возможно вам будут полезны:

