Предел функции по Гейне и по Коши

Оглавление:

Предел функции по Гейне и по Коши

Пределы функции Хейна и коши. Если вы определяете *(Y=} (x) в некотором бесконечном множестве{x} и делаете a точкой бесконечных линий (—OO,+OO), то она, вероятно, не принадлежит множеству{x}, но если a находится в любой 6 окрестности этой точки A. *Это означает, что O является точкой разрыва множества{x}. ** Генрих Эдуард Гейне-немецкий математик (1821-1881). ‘**B зависит от e, поэтому его можно записать как b=6 (e). Например, интервал (a, 6) может служить множеством{x}; в этом случае точка a является граничной точкой интервала, и она ему не принадлежит, но любой 6-ближайший сосед a является граничной точкой указанного

интервала. Другим примером множества{x}, где задана функция^(x), является множество всех рациональных чисел, принадлежащих интервалу (a—b, a-|-d), где точка a была выброшена. Кстати, в случае интервала 6>0 (a-6, a — \ — b), где точка a выбрасывается, она называется p R O K O l o t o th6 o Crosspoint a. О П Р Е Д Е Л Е и Е1(П Р Е Д Е Л Ь Ф УН К и по) Г * Е Н Е’. Число B называется p R e d e l o m (или PR e d e l L N s m s n a h e n) функцией y=} (x), если точка a(или x — >a), значение аргумента X1, XG, в любой последовательности..,

xn, состоящий из числа xn, отличного от a, соответствующей последовательности значений функции 1 (x (), /(XG),…, ^(HP) … Людмила Фирмаль

сходиться к числу B. О П Р Е Д Е Н И Е * 1(П Р Е Д Е Л Ь Ф ункц и ПО к Ош и). Число B называется функцией y p R e d e l o m (или p R e d e l L N s m z n a h e N I E m)?если (x) является точкой a (или x->a) и существует положительное число 6t,a, соответствующее любому положительному числу e, то для всех значений аргумента x, удовлетворяющих условию 0<|x—a|<6, неравенство//(x)—B\6-ha-.Но Глава 3. Теория пределов Прежде чем доказывать эквивалентность определений 1 и 1, давайте дадим некоторые комментарии, объясняющие значение этих определений. З а м е ч а н и Е1. Мы

подчеркиваем важность схватывания требований определения 1 и обязывания элементов последовательности значений аргумента CP быть различными, а также сходных требований в определении 1, поскольку это требование может заключаться в том, что функция y=} (x) не определена в пункте И. Без этого требования становится невозможным использовать предельную функцию для определения производной функции. На самом деле, от парня. Вы можете видеть, что производная от 1

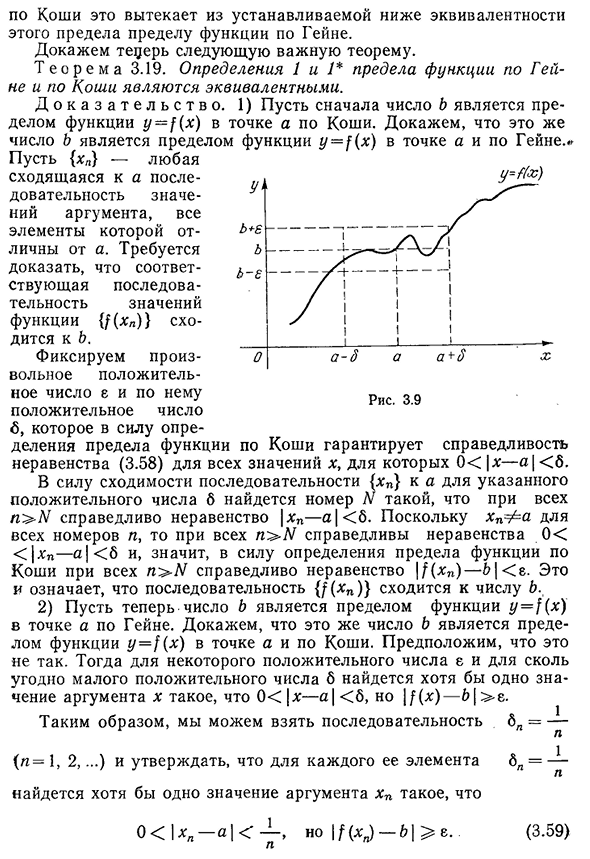
функции/(x)}'(a)является пределом x — >a для следующей функции: Очевидно, что эта функция P (x) не определена в точке a,что вызвано сущностью экземпляра. З а м е ч а н и Е2. Этот набор{x}требует только, чтобы в проколотой окрестности точки B был хотя бы один элемент A.An примером множества{x}является множество всех элементов массива в фиксированной окрестности точки a=6. З а м е ч а н и Е3. Условия, появляющиеся в определении 10< / x—»|(3.58), является、 З а м е ч а н и Е 4. 1 * определение пределов функции Коши можно перефразировать следующим образом: число B является P R e d e l L N s M z n a h e N I}(x)t o h to e данная функция точности}(X)аппроксимирует значение точности e(рис.). 3.9). З а м е ч а н и Е 5. Заметим, что

функция/(x) может иметь в точке «t o l L K o один предел». На практике, чтобы определить пределы функции Хейна, это следует за единственностью пределов последовательности {^(CP)} и определяет пределы функции§4. Предел функции 111 Значение со всех мест-И. Требуется соответствующее последовательное значение По Коши, это продолжается от эквивалентности этого предела к пределу функции Хейна, установленной ниже. Докажем следующие важные теоремы. 3.19 определение пределов функций по Хейну и коши 1 и 1эквивалентны. Д О К а з а т е л ь с Т В О. 1) Коши сначала доводит число B до предела функции y=f(x) точки A. чтобы доказать, что число L является пределом функции

y=[(x) точки, пусть{XL}сходится к последовательности;Из личного пункта докажите аргумент, текущий выходной функции{DHD}. Людмила Фирмаль

Исправьте все положительные значения То же самое и на Гейне.» На рис. 39 приведено положительное число b, которое гарантирует справедливость неравенства (3.58) для всех значений x путем определения пределов функции Коши, а 06. Таким образом, мы можем взять последовательность b » = — (и=1, 2,…)И утверждать его для каждого из своих элементов b » = — так, чтобы было хотя бы одно значение аргумента CP 0< / х» — а / < —, п Но| / (x») — b / >e. (3.59)112 Глава 3. Теория пределов Левая часть неравенства (3.59) означает, что последовательность{xn}сходится к a и состоит из больших чисел. Однако в этом случае, согласно определению предела по Гейне, соответствующая последовательность значений функции {[(xn)} должна сходиться к числу B, что является правильным неравенством (3.59). Нам дали очко A.In 1°, и приведите пример функции с предельным значением, которого нет. Функция/(x)=C=sopz1

имеет предел, равный C в каждой точке A бесконечной прямой. Фактически, для любого значения аргумента x разность [(x) — C равна нулю, и поэтому|[(x) — C|и всех значений аргумента(в данном случае e>0 2°в определении предела Коши. Функция/(x)=x в любой точке A бесконечной прямой имеет предел, равный a. фактически, в этой функции последовательность значений аргумента и соответствующие значения функции одинаковы, поэтому, когда последовательность{CP}сходится к a, последовательность {/(CP)} также сходится к A.It сходится к 3°. Значение функции Дирихле O (x) является рациональной точкой, ноль-неразумной точкой, и нет предела любой точке бесконечной прямой. Это объясняется тем, что в случае

последовательности сходимости значений рациональных аргументов предел последовательности соответствующих значений функций равен единице, в случае последовательности сходимости значений иррациональных аргументов соответствующее значение функции равно единице. Здесь мы вводим понятие функции d n O S t o r o n e g o (т. е., правого или левого)предела в данной точке A. здесь это множество{x}любого b>0 должно иметь по крайней мере один элемент, принадлежащий интервалу (a, a-|-b) [интервал (a—b, a)]. О П Р Е Д Е Л Е Н и Е2(Р рабы й [таксации й] п р е Д Е Л Ь Н О К тионс о г о). Число S равно p p P P p R e d e l o m[levy m p P R e d E l o m]f u n K t I y=[(x)) для любой последовательности значения аргумента A{xn}в точке A является включительным. О п р ЕД е л я Е2(право г

[Леви Г] П Р Е Д Е Л Ф у Н К цию С К Ош я). Число B называется p R a[l v s m p R e d e l o m]f n K c I y=[(x) t для точки a, для любого положительного числа e, для всех значений аргумента x»§4 предел функции 113. Удовлетворяют условию a<.xa-{- $x — +A-O или более короткий символ[(a+0)=B[/(a-0)=&]. Доказательством этой теоремы является аргумент: доказана эквивалентность теоремы и полная аналогия определения 3.19*с 2: 2, необходимая для всех рассуждений, в которых она сделана. * Очевидно, верно и обратное:если функция/(x) имеет предел, равный B в точке a, то существует»предел как правого, так и левого в точке A} (x), и оба они равны B. В качестве примера рассмотрим следующую функцию /(х)=з§п= х ‘ +1 , Отчет, 1-1., для Х>О, Х=О, х<0.

Критерий Коши сходимости последовательности	Критерий Коши существования предела функции.
Понятия переменной величины и функции	Почленное интегрирование степенного ряда