Оглавление:





Предел функции
- Ограничение функции 1. Ограничения на функции в определенных точках Определите функцию y = f (x) вблизи точки xq, возможно, исключая саму точку xq. Сформулируйте два эквивалентных определения функциональных ограничений в точке. Определение 1 («Язык последовательности» или по Гейне). Для последовательности допустимых значений аргумента xn, если n∈N (xnΦ £ 0)> xo (т.е. limxn = h: o), соответствующая последовательность значений функции f (xn) 71 6 N Сходится к числу A (то есть lim f (xn) = A).
Геометрический смысл функциональных ограничений: lim / (rr) = A Х- »Хо Для каждой точки π, достаточно близкой к точке x0, соответствующее значение функции должно быть как можно меньше с числом A Определение 2 («Язык £> <5» или Коши). Число A называется пределом функции в точке x0 (или x -4 x0), если такой положительный существует для любого положительного e Для всех xΦx0, удовлетворяющих неравенству -jo | <6, выполнено неравенство \ f (x) -A \ <e. Напишите lim f (x) = A.
В этом случае lim f (x) = A или f (x) -4 A описывается как x-> x0. Людмила Фирмаль
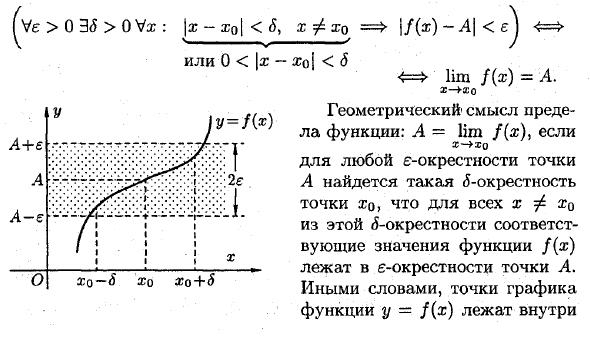
Это определение можно легко записать следующим образом:\ Ve> 0 36> 0 Ва :: \ x-xQ \ <6, Или 0 <\ x- у-ф (х) xq — 8 часов hfhr => If (x) -A \ lim f (x) = A г-FXO Значение ограничения геометрической функции: A = lim f (x)), если х- »зо Для любой £ окрестности точки A существует ^ окрестность точки, поэтому для каждого xΦx0 из этой окрестности соответствующее значение функции f (x) находится в окрестности е точки A. То есть лежащий в графе пункт (x) функции y = f
Прямая линия y = A-f e, y = A — полоса шириной 2e, разделенная e. Очевидно, мы пишем 6 = 6 (e), потому что величина S зависит от выбора £. Пример: 1) Докажите, что lim (2x-1) = 5. x- ♦ Возьмем любое e> 0, найдем 6 = (5 (c)> 0 и неравенство | x-3 |
| Функция | Бесконечно малые функции (Б.М.Ф.) и основные теоремы о них |
| Последовательности | Связь между функцией, ее пределом и бесконечно малой функцией |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
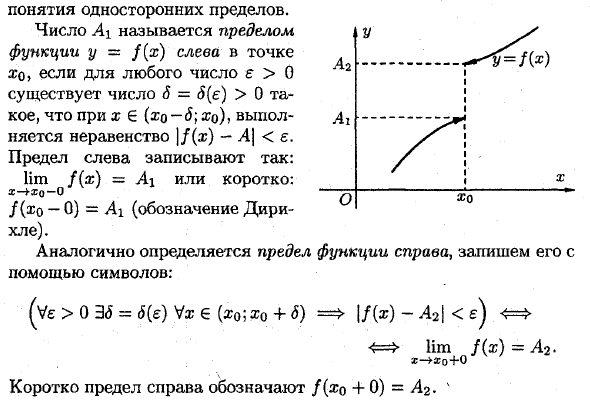
Ограничения на левую и правую функции называются односторонними ограничениями. Очевидно, что если lim / (x) = A существует, X-4Xo Кроме того, существует одностороннее ограничение как A = A \ -A2. Обратное также верно. Если существуют оба предела f (xo-0) и f (xo + 0), и они равны, то пределы A = lim f (x) и A = Dho-0). X-> Ho В случае A \ ΦA-2) lim f (x) не существует. X— ”Хо 3. Ограничение функций в x OS Предположим, что функция y = f (x) определена в интервале (-oo; oc).
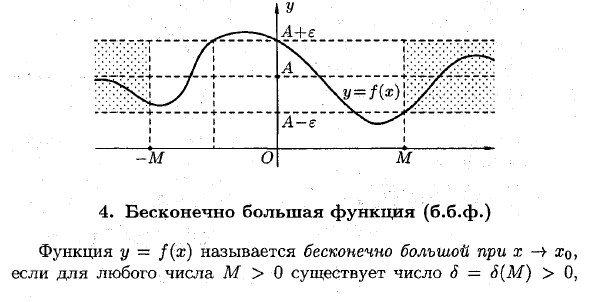
. > M, неравенство | / (x) -A \ 0 3M> 0 Vx: | x |> M | / (x) -A \ + оо A = lim / (x). Геометрический смысл этого определения заключается в следующем: X — U —oo Для Vs> 0 3M> 0, для x € (-ox; -M) или x € (L /; + oo) соответствующее значение функции f (x) находится вблизи e точки A , Он находится на полосе шириной 2e и окружен линией y-A + e pn = A-e.
Число A называется пределом функции f (x) при x → ∞, если существует число M = M (r)> 0 такое, что все x удовлетворяют неравенству | x | Людмила Фирмаль
Функция бесконечности (BFB) Функция y =} (x) называется бесконечностью для x> 0, если число 8 = 6 (M)> 0 существует для любого числа M> 0. Напишите <0, неравенство | / (x) |> M. lim f (x) = oo для всех x, удовлетворяющих неравенству 0 <| x-xo x-> ®o Или f (x) — YO для IЧHo. Простой: (YM> 0 3 (5> 0 yl: \ x-x0 \ <6, xφx0 ==> | / (x) |> m) lim / (x) = oo. X— ¥ Ho Например, функция y = —b.p. В х 2. X ~ A Если f (x) бесконечно, как x xo, и принимает только положительные значения, lim f (x) = -foe; X—> Io
Только отрицательные значения, lim f (x) = —oo. X—> Хо Функция y-f (x), определенная целой линией, называется бесконечностью относительно x °. Для любого числа M> 0, если существует число N = AG (M)> 0 такое, что все x удовлетворяются> Ny, выполняется неравенство \ f (x) > M. (Mind> 0 3N> 0 уже: | x |> LH => | / (x) |> m) lim / (x) = oo. х-йо Например, у = 2x имеет BBF. в х ос. Если аргумент w, идущий в бесконечность, принимает только натуральные значения, т. Е. W ˆ N, то соответствующая BBF бесконечно большая последовательность.
Например, последовательность с vn = n2 + 1, n∈N является бесконечно большой последовательностью. Очевидно, что в окрестности всех точек BBF x0 нет границ в этой окрестности. Обратное неверно. Неограниченная функция не может быть b.f. Однако если lim f (x) = A (A — конечное число), функция X- * ho f (x) ограничено окрестностью xq. Конечно, условие x xo | f (x) -A | \ <\ A \ + £ для x € (a0- £ \ x0 + s). Это означает, что функция f (x) ограничена.

