Бесконечной числовой последовательностью называется совокупность чисел, каждому из которых присвоен определённый порядковый номер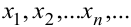 
Числовая последовательность задаётся общим членом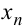 
, записанным в виде функции номера: 
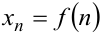. Например, последовательность 
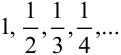задаётся её общим членом 
.
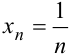Число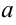 
называется пределом последовательности 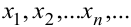, если для всякого сколь угодно малого положительного числа 
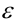(ипсилон,) найдётся такое положительное число 
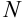, что 
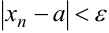при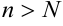 
.
В этом случае пишут
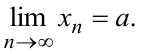
(Читается: предел последовательности равен 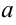при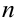 
стремящемся к бесконечности).
Числовая последовательность 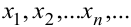называется бесконечно малой, если её предел при 
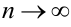равен нулю. Так, числовая последовательность с общим членом 
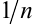является бесконечно малой.
Числовая последовательность называется бесконечно большой, если для каждого сколь угодно большого положительного числа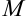 
можно указать такое число 
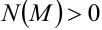, что для всех значений 
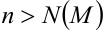выполняется неравенство 
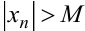. В этом случае пишут: 
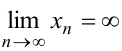. Примером бесконечно большой последовательности является последовательность натуральных чисел 
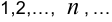Здесь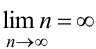 
.
Предел постоянной величины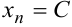 
равен самой этой величине, так как неравенство 
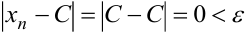выполняется при любых 
.
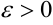Не всякая числовая последовательность имеет предел, например, последовательность с общим членом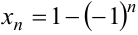 
. Последовательность имеет вид: 2,0,2,0,2,0,… С ростом номера члены числовой последовательности не приближаются к какому-то одному числу, для них нельзя указать число 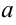, для которого выполнялось бы неравенство 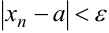при .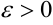
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
| Уравнения плоскости в пространстве |
| Эллипс, гипербола, парабола |
| Предел функции при x>a |
| Предел функции при x>∞ |
