Оглавление:
Правило Лопиталя
Правило Лопиталя позволяет раскрыть неопределённости вида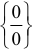 
, 
.
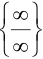Правило Лопиталя. Пусть имеем частное двух функций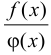 
, где 
и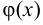 
определены в 
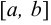, имеют конечные производные 
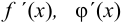в этом промежутке, причём 
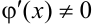. Тогда если обе функции бесконечно малые или бесконечно большие при 
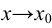и существует 
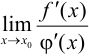, то существует также 
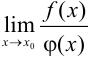и эти пределы равны, т. е. 
.
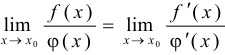Задача №59.
Найти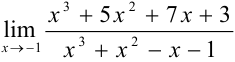 
, применив правило
Лопиталя.
Решение:
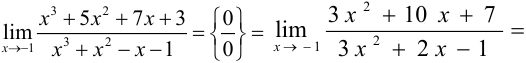
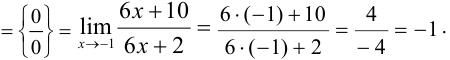
Задача №60.
Найти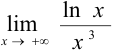 
, применив правило Лопиталя.
Решение:
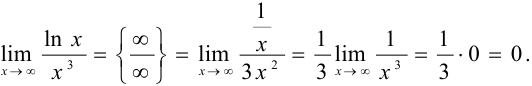
Неопределённости вида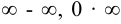 
с помощью преобразований приводятся к неопределённостям вида 0/0 или 
.
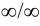Задача №62.
Найти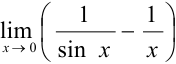 
, применив правило Лопиталя.
Решение:
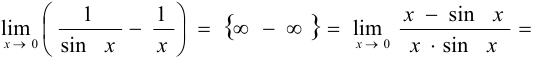
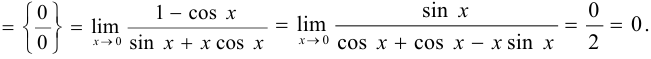
Неопределённости вида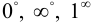 
путём логарифмирования приводятся к неопределённости вида 
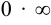, затем к неопределённости 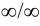или 0/0, и потом можно применить правило Лопиталя.
Задача №63.
Найти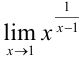 
.
Решение:
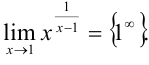Сделаем замену 
.
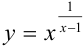Прологарифмируем обе части равенства, получим: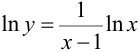 
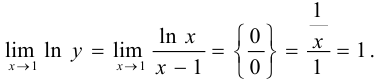
Имеем: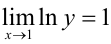
или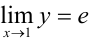 
, т. е. 
.
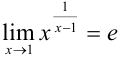Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
