Оглавление:
В предыдущей главе мы учились находить пределы различных функций. Но всегда ли это возможно? Пусть нужно вычислить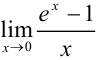 
. Любой предел мы начнем раскрывать с оценки: окажется, что перед нами неопределенность вида 
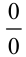. И никакой из ранее известных нам методов в данном случае неприменим.
Тогда на помощь придет правило Лопиталя. Под правилом Лопиталя
понимают прием раскрытия неопределенностей вида 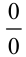или 
.
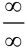Теорема (правило Лопиталя). Для вычисления предела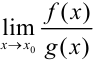 
, где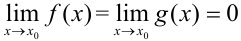 
, достаточно найти предел отношения производных данных функций (если он существует), т.е. 
.
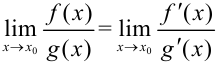Замечание. 1. Правило Лопиталя справедливо также для случаев
- неопределенности вида 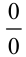при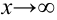
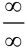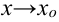; - неопределенности вида при
и .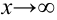
2. Правило Лопиталя может быть применено последовательно несколько раз для раскрытия неопределенностей вида 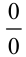или .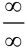
Рассмотрим примеры нахождения пределов функций с использованием правила Лопиталя.
Пример №13.5.
Вычислите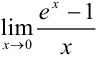 
.
Решение:
Поскольку в примере встречается неопределенность вида 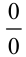, можно применить правило Лопиталя:
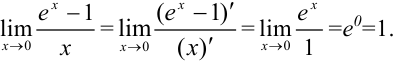
Ответ: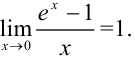 
Пример №13.6.
Вычислите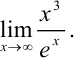 
Решение:
Поскольку в примере рассматривается неопределенность вида 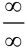, можно применить правило Лопиталя:
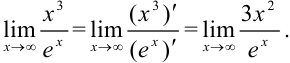Снова получили неопределенность вида 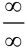, следовательно, можно применить правило Лопиталя еще раз:
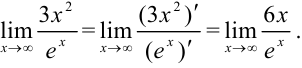Повторно применяя правило Лопиталя, получим
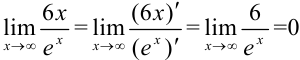, т.к. 
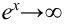при .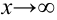
Ответ: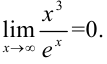 
Пример №13.7.
Вычислите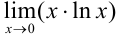 
.
Решение:
Поскольку при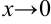 
функция 
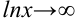, то имеет место неопределенность вида 
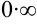и правило Лопиталя применить нельзя. Попытаемся преобразовать выражение, стоящее под знаком предела: 
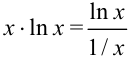. Тогда под знаком предела будет неопределенность вида 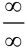, к которой правило Лопиталя применимо:
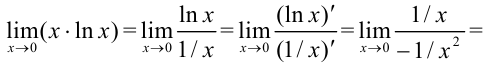
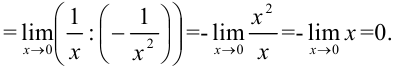
Ответ: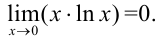 
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Понятие производной высших порядков |
| Понятие дифференциала высших порядков |
| Признаки возрастания и убывания функции |
| Понятие точек экстремума и экстремумов функции |
