Оглавление:

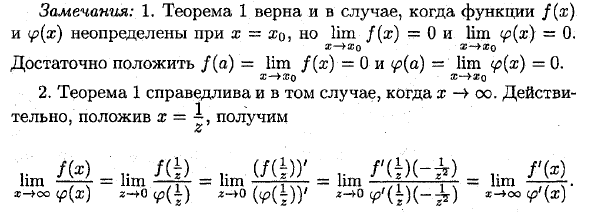

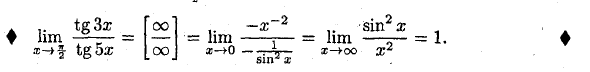
Правило Лопиталя
- Правило капитала к р Рассмотрим способы раскрытия неопределенности формата j, Это основано на использовании производных. Теорема 1. Предположим, что функции f (x) и (p (x) непрерывны, дифференцируемы вблизи точки x0 и исчезают в этой точке: f (xo) = φ (xo) = 0. x0 X0 ip (x) x-> xo 4> (x)
Примените теорему Коши к M сегментам f (x) и tp (x) [a; o; x]> около точки x0. Тогда = с находится между хо и х. Если f (x0) — xo ip (X) c-> xo (X) Легко полученное выражение читается следующим образом: «VПримечания: 1. Теорема 1 состоит в том, что функции f (x) и
Пределы двух бесконечно малых отношений равны пределам отношения этих производных, если они существуют. Людмила Фирмаль
| Теорема Коши | Раскрытие неопределенностей различных видов |
| Теорема Лагранжа и ее следствия | Возрастание и убывание функций |
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
- (x) = 0 достаточно. X— * XQ X—> XQ 2. Теорема 1 справедлива для х оо. На самом деле, если вы установите x = A: lim u = lim i! > = lim w w. Теорема 1 может быть применена повторно, если производные f ‘(x) и . км- = лим- = лим — у— x- + x0 ip (x) Z- + X0 (f [X) r-bad ip «[X) И т. Д. Пример: х-1 г X до 1 лим. -: — а: а; 1) найти лим r (* «*) ‘r 1 = lim ——- lim — = 1. xs (hthu * -i1pzh + 1 2) Найти предел 1 ~ cЯ | 6: c. 2а: 2 1-cos 6a: lim ——— g — x ~> o 2×2 6 грех 6x-хм 3 .. 6 cos 6a: = -lim — = 9. 2 х-> около 1 ♦
Теорема 1 позволяет выявить неопределенность вида -. Сформулируйте без доказательства неограниченной теоремы о Семенной сплит. 00 Теорема 2. Предположим, что функции f (x) и ip’ix) Φ0. Lim ■ если есть ограничения, X- + XO ‘h X- + XO (p (X) HM U = Lim W x- * x0 H> \ X) * -> xo Y (x) Правило расчета пределов, выраженное в теоремах 1 и 2, называется правилом Лопигала.
Пример: поиск лим. * -> f.tg5s -2 тг 3 а: тг бх преступление ОО 00 -X ободок ободок = Оправа х-> оо х ‘ грех2 х Людмила Фирмаль

