Теорема. Система 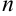 линейных уравнений с
линейных уравнений с 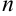 неизвестными имеет единственное решение, если определитель, составленный из коэффициентов при неизвестных, отличен от нуля.
неизвестными имеет единственное решение, если определитель, составленный из коэффициентов при неизвестных, отличен от нуля.
Это решение находится по правилу Крамера:
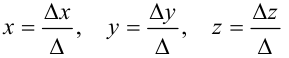
где  — определитель, составленный из коэффициентов при неизвестных;
— определитель, составленный из коэффициентов при неизвестных;
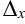 получается из определителя
получается из определителя  заменой столбца коэффициентов при
заменой столбца коэффициентов при 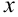 столбцом свободных членов;
столбцом свободных членов;
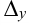 получается из определителя
получается из определителя  заменой столбца коэффициентов при
заменой столбца коэффициентов при 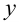 столбцом свободных членов;
столбцом свободных членов;
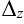 получается из определителя
получается из определителя  заменой столбца коэффициентов при
заменой столбца коэффициентов при 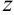 столбцом свободных членов.
столбцом свободных членов.
Пример №4.1.
Решите систему уравнений по правилу Крамера: 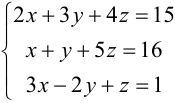
Решение:
Составим определитель  из коэффициентов при неизвестных и вычислим его:
из коэффициентов при неизвестных и вычислим его:
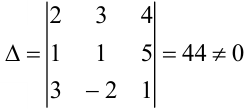
Определитель  отличен от 0, следовательно, система имеет единственное решение.
отличен от 0, следовательно, система имеет единственное решение.
Для его нахождения вычислим 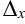 ,
, 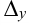 и
и 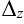 :
:
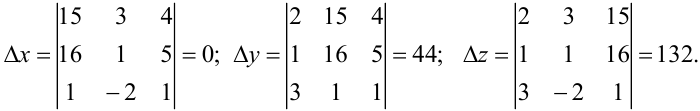
По правилу Крамера найдем неизвестные:
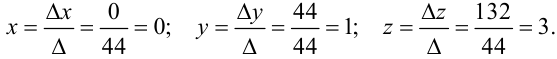
Замечание. Для проверки правильности решения системы уравнений необходимо подставить найденные значения неизвестных в каждое из уравнений данной системы. При этом, если вес уравнения обратятся в тождества, то система решена верно.
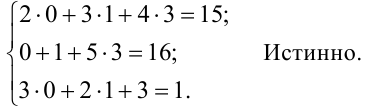
Итак, решение системы найдено правильно.
Ответ: 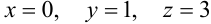 .
.
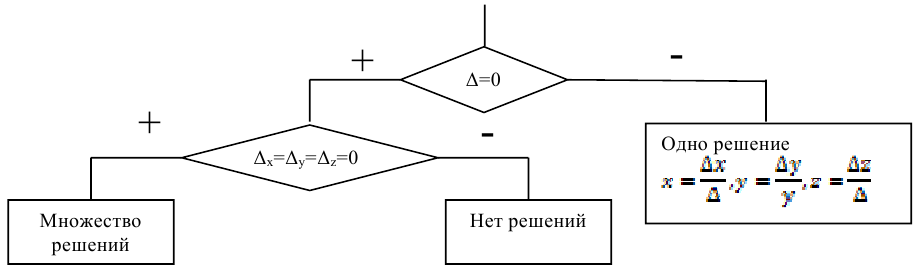
Для нахождения числа решений системы 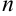 линейных уравнений с
линейных уравнений с 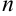 неизвестными можно использовать следующую блок-схему:
неизвестными можно использовать следующую блок-схему:
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Понятие ранга матрицы. |
| Понятие решения системы линейных уравнений. |
| Метод Гаусса решения систем линейных уравнений. |
| Критерий Кронеккера-Капелли совместности систем линейных уравнений. |

