Оглавление:
Правило для исследования функции на экстремум вторым способом
- Найти
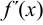 .
. - Решить уравнение
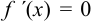 .
. - Исследовать знак второй производной. Если в этих точках
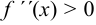 , то в этой точке будет минимум, а если
, то в этой точке будет минимум, а если 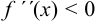 , то в ней будет максимум. Если
, то в ней будет максимум. Если 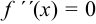 , то исследование надо провести по первому правилу.
, то исследование надо провести по первому правилу.
Чтобы определить наибольшее и наименьшее значение функции на отрезке, надо:
1) определить критические точки функции;
2) вычислить значение функции в критических точках и на концах отрезка;
3) наибольшее из значений найденных в и. 2 будет наибольшим, а наименьшее — наименьшим значением функции на отрезке.
Если в рассматриваемом интервале имеется единственный экстремум, то в критической точке функция достигает наименьшего или наибольшего значения, смотря по тому, будет ли в этой точке минимум или максимум.
Задача №65.
Исследовать функцию 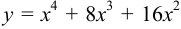 на экстремум и найти её наибольшее и наименьшее значение на отрезке [-3; 1].
на экстремум и найти её наибольшее и наименьшее значение на отрезке [-3; 1].
Решение:
Область существования — бесконечный интервал 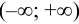 .
.
1. Находим первую производную:
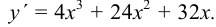
2. Для определения критических точек решаем уравнение
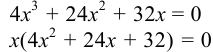
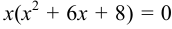 , откуда
, откуда 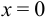 и
и 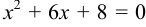 .
.
Решая это уравнение, имеем точки 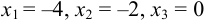 .
.
Применим первое правило.
3. Критические точки разбивают область существования функции на интервалы: 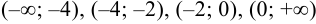 .
.
4. Для исследования в них знака первой производной нужно в каждом интервале выбрать произвольную точку. В первом интервале 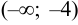 возьмём точку
возьмём точку 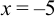 , во втором —
, во втором — 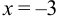 , в третьем —
, в третьем — 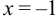 , в четвёртом —
, в четвёртом — 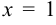 .
.
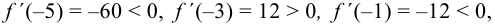
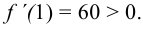
5. Последовательность знаков первой производной в рассматриваемых интервалах запишется так:
при 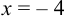 имеем минимум,
имеем минимум, 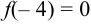 ,
,
при 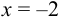 — максимум и
— максимум и 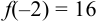 , а
, а
при 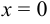 — минимум и
— минимум и 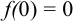 .
.
Решим задачу вторым способом, т. е. исследуем функцию па экстремум с помощью второй производной. У нас критические точки: -4, -2, 0.
Найдём вторую производную функции 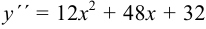 .
.
Определяем знак второй производной в каждой критической точке:
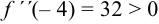 , при
, при 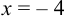 функция имеет минимум;
функция имеет минимум;
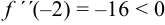 , при
, при 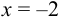 функция имеет максимум;
функция имеет максимум;
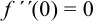 , при
, при 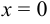 функция имеет минимум.
функция имеет минимум.
Найдём наименьшее и наибольшее значение функции на отрезке [-3, 1]. Этому отрезку принадлежат две критические точки: 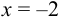 и
и 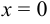 .
. 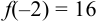 ,
, 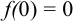 . Для решения вопроса о наибольшем и наименьшем значениях функции надо рассмотреть значения функции на концах отрезка [-3,1]:
. Для решения вопроса о наибольшем и наименьшем значениях функции надо рассмотреть значения функции на концах отрезка [-3,1]: 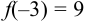 ,
, 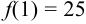 . Отсюда следует, что наибольшее значение функция имеет на правом конце рассматриваемого отрезка в точке
. Отсюда следует, что наибольшее значение функция имеет на правом конце рассматриваемого отрезка в точке 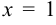 ,
, 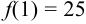 , а наименьшее — в точке
, а наименьшее — в точке 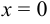 ,
, 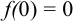 .
.
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:

