Оглавление:
Правила вычисления. Условие значимости цифр
Результаты анализа должны быть вычислены с той же точностью, что и выполненные измерения. С этой целью при расчете результатов всегда сохраняют одну лишнюю цифру по сравнению с числом цифр в конечном результате, т. е. используют значащие цифры. Значащими называют все достоверно известные цифры плюс первая из недостоверных. В конечном результате число округляют с учетом значащих цифр, а лишнюю цифру отбрасывают. При представлении числа, выражающего результат измерения или вычисления с учетом значащих цифр, следует помнить, что нули в начале числа незначимы (в числе 0,0015 — две значащие цифры, в 0,0150 — три); нули, стоящие между цифр — всегда значимы. При представлении чисел с нулями, стоящими после цифр, значащие цифры должны быть четко показаны, например, степенным выражением (5,00* 10“ — три значащие цифры) или указанием нуля после запятой (200,0 — четыре значащие цифры).
При проведении любого расчета нужно уметь округлять полученный результат. Если за первой недостоверной цифрой следует цифра 5, округление проводят до ближайшего четного числа. Например, число 12,245 следует округлить до 12, 24; число 12,255 -до 12,26.
Рассмотрим некоторые правила округления для основных арифметических действий, наиболее часто встречающихся при расчете химических равновесий и результатов химических методов анализа.
Сложение и вычитание. Значимость суммы или разности определяется значимостью числа с наименьшим числом десятичных знаков. Например, при сложении чисел 4; 0,21 и 22,3 значимость определяется недостоверностью числа 4. Тогда сумму чисел 26,51 следует округлить до 26. При отбрасывании цифры 5 округляют до ближайшего четного числа. При сложении чисел со степенями приводят показатели степеней к наибольшему числу, а далее поступают в соответствии с приведенным правилом. Например: сумма чисел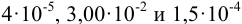 
, преобразованных в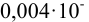 
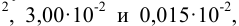должна быть выражена числом 
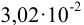(значимость суммы определяется значимостью числа 
).
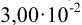Умножение и деление. Число значащих цифр произведения (или частного) величин, измеренных с разной точностью, определяется значимостью сомножителя с наименьшим числом значащих цифр. Например, перемножение чисел 1,5 и 2,35 дает произведение 3,525, которое представляют числом с двумя значащими цифрами, т. е. 3,5. С учетом приведенных правил рекомендуется округлять результат после проведения всех арифметических действий.
Возведение в степень. Относительная недостоверность результата возведения в степень увеличивается в число раз, равное степени (то есть при возведении в квадрат — удваивается).
Извлечение квадратного корня. Относительная недостоверность результата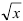 
вдвое меньше относительной недостоверности числа х, поэтому в некоторых случаях после извлечения корня число значащих цифр увеличивается. Например 
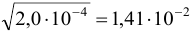, поскольку относительная недостоверность для значащих цифр числа 
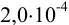равна ±0,1, а результата извлечения корня: ±0,1/2 = ±0,05, поэтому в его значащие цифры включается вторая после запятой.
Логарифмирование. Число значащих цифр в мантиссе равно числу цифр, которое содержал нестепенной член числа. Характеристика логарифма, определяющаяся порядком логарифмируемого числа, не входит в число значащих цифр, например:
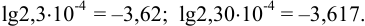
Абсолютная недостоверность логарифма примерно в 2,5 раз меньше относительной недостоверности числа под логарифмом. Например, если относительная погрешность логарифмируемой величины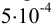 
, то точность логарифма 
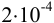. Для антилогарифмов число значащих цифр, соответственно уменьшается, например:
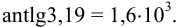
Следует помнить, что округление проводят после окончания всех математических действий, всех расчетов. Результат измерения (определения) и его погрешность следует выражать числом с одинаковым количеством цифр после запятой. Например, представляя средний результат анализа, имеющий четыре значащих цифры и две из них после запятой, при указании границ доверительного интервала после запятой должно быть не более двух цифр:
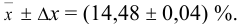
Пример №1.1.
Раствор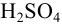 
для создания среды в титримет-рии приготовили, сливая остатки трех растворов: 50 мл, 5,25 мл и 14,5 мл с разными концентрациями. Определите объем полученного раствора.
Решение:
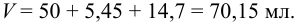
Наименьшее число значащих цифр в объеме 50 мл, поэтому округленный результат содержит 2 значащих цифры: V= 70 мл.
Пример 1.2.
Для раствора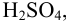 
полученного по условию примера 1.1 (количество вещества 
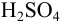в 50 мл равно 
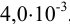, в 5,25 мл — 
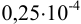, а в 14,5 мл — 
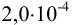моль) вычислите: а) общее количество вещества 
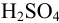; б) молярную концентрацию.
Решение:
а) При сложении взятых количеств кислоты следует уравнять показатели степени, приводя их к наибольшему числу:
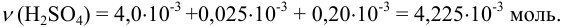
Округление проводим по первому слагаемому, имеющему наименьшее число десятичных знаков, т. е.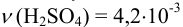 
;
б) концентрация серной кислоты: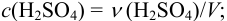 
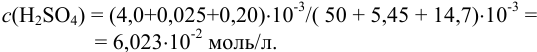
Округление проводим до 2-х значащих цифр, ориентируясь на числа 50 и 4,0, тогда результат расчета концентрации:
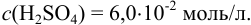
Пример 1.3.
Определите массовую долю серы в сухом угле, если по данным весового анализа из навески угля 2,6448 г (с влажностью 2,58 %) получено 0,3248 г весовой формы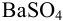 
.
Решение:
После подстановки величин в расчетную формулу (гл.7) получаем:
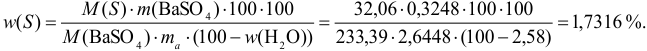
Результат округляем до сотых долей процента, ориентируясь на число 2,58 с наименьшим числом значащих цифр.
Пример 1.4.
Вычислите и округлите результат:
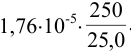
Решение:
При вычислении получаем величину:
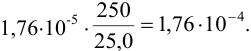
Все числа, входящие в формулу, имеют одинаковое число значащих цифр, но абсолютные и относительные недостоверности их отличаются. При отсутствии в задании абсолютных недостоверностей этих трех чисел считаем их равными ±1 в последней значащей цифре каждого числа. Тогда относительные недостоверности составят:
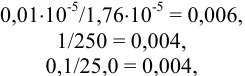
а их сумма равна: 0,006 + 0,004 + 0,004 = 0,014.
Абсолютная недостоверность результата равна:
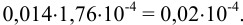
Поскольку недостоверность в последней цифре превышает 1, рекомендуется округлить результат до 2-х значащих цифр, а именно: до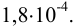 
Пример 1.5.
Вычислите pH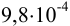 
М раствора сильной кислоты НА.
Решение:
Для сильной кислоты:
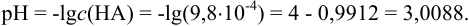
В коэффициенте величины с(НА) всего две значащие цифры (9,8), поэтому мантиссу округляем до двух цифр: pH = 3,01.
Эти примеры взяты со страницы примеров решения задач по аналитической химии:
Решение задач по аналитической химии
Возможны вам будут полезны эти страницы:
