Правила вычисления производных, связанные с арифметическими действиями над функциями

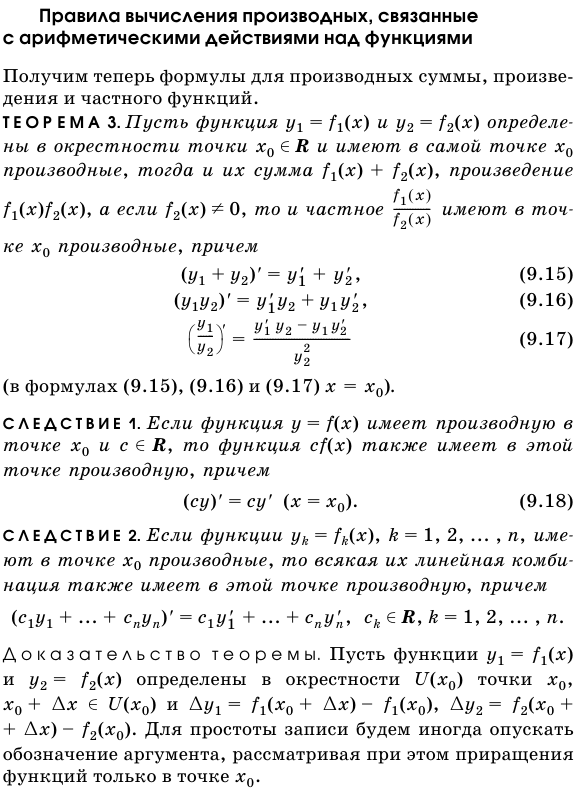
Правила вычисления производных, связанные с арифметическими действиями над функциями

Правила вычисления производных, связанные с арифметическими действиями над функциями. Она у меня есть. Теорема 3. Определим функции y = A \(x) и y2 = A2 (x) в окрестности точки x∈K и получим производную в самой точке x, а их сумму A (x)+ / 2 (x), ke X производные, далее (Формула (9.15), (9.16) и (9.17) x = x). Следствие 1.Если функция y = A (x) имеет производную в точках x и c∈K, то функция cA (x) также имеет производную в этой точке、 Следствие 2.Функция yk = f (x), V = 1, 2,… Доказательство теоремы. Предположим, что функции y1 = Ar (x) и y2 = A2 (x) определены в окрестности точек x〜и (x).х+ Ах∈УБ + Ax) A2 (x).для упрощения описания нотация аргумента может быть опущена, учитывая приращение функции только в точке X. если г = г + У2.

Здесь мы получаем сумму, произведение и формулу производной определенной функции. Людмила Фирмаль

• Получить Dx f оттуда Здесь мы передаем ограничение как хχ^, и заметим, что из-за наличия производных функций Y и Y2 в точках x0 ограничение на правой стороне этого равенства существует и равно y + y2, то есть на левой стороне его также есть ограничение Y’, и y ’ = Y2, т. е. если y = у У2, затем аналогичным способом Наличие производной f2 (x) означает непрерывность функции f2 в точке x0. NT Du2=; далее Поэтому идите до предела Дх ^ о равенстве, полученном из Наконец, если y = и/ 2 (x) Φ、 Поэтому, когда Дχ^, напомним, что существование производной означает непрерывность функции, таким образом、 Фактически мы получаем Um Du2=, y ’= 2, то есть формулу<sup class=»reg»>®</sup>U2.

• Формула (9.17) также была доказана. если вспомнить c ’=(см. Пример 9.1 из§ 1), то результат 1 следует сразу же после(9.16), а результат 2 сразу же получается математической индукцией из формул(9.15) и(9.18). Я не уверен. Замечание. Вы можете установить соответствующее свойство производной инфинитива, используя свойство бесконечного предела, связанного с арифметической операцией функции (см.§ 5.1).Например, если существует конечная производная y1 (x) и бесконечная (Для некоторых кодов) является производной от y2 (x), а функция y (x)= y-Dx)+ y2 (x) в x имеет бесконечную производную того же знака. Например, если У2(х)= + то, Г ’(Х)= + го. На самом деле, отель Du = Du1 + Du2.Так.

Если функция имеют производные в точке x, то их линейные комбинации также имеют производные в этой точке. Людмила Фирмаль

• Если существует конечный предел 11t-r—, и 11t-r2 = Образцы. 1. г = е B1n х-2х сов x. By Формула(9.15), (9.16) и(9.18)、 2. пусть y = x. так как x Затем, согласно формуле 3.Аналогично, если y = c1§ X Свойство(9.15) (9.18) переносится на разность функций. При тех же предположениях о Дифференцируемости в точке X. Например, вычислите разность произведения V = V1U2. У1 ^ = _Y1,У2 ^ = _y2. Остальные Формулы также будут доказаны. Теорема 4.Пусть функция V = f (X) непрерывна и строго монотонна в окрестности тонкого X.、 Если X = x, то есть свободный _x^. обратная функция togba X = / 1(Y) является необязательной для тонера Y = /(x).

Смотрите также:

Предмет математический анализ

Геометрический смысл производной и дифференциала.	Производная обратной функции.
Физический смысл производной и дифференциала.	Производная и дифференциал сложной функции.