Оглавление:
Рациональные числа. Правила перевода рационального числа из обыкновенной дроби в периодическую и обратно
Опр.1. Рациональным называется число, представимое в виде обыкновенной дроби р/q, где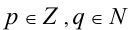 
. Так как любую обыкновенную дробь путём сокращения можно привести к несократимому виду, то, как правило, в определение рационального числа сразу добавляют условие несократимости дроби, что не влияет на суть определения.
Опр. 2. Рациональным называется число, представимое в виде десятичной бесконечной периодической дроби.
Теорема 1. Определения 1 и 2 эквивалентны (без доказательства). Множество рациональных чисел принято обозначать буквой Q (от латинского ‘quotient‘ — частное), а название рациональных чисел происходит от латинского ‘ratio’ — отношение. Заметим, что любое целое число n является рациональным, так как его можно представить в виде обыкновенной дроби n = n/1 . С учётом этого имеем: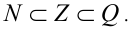 
В силу теоремы 1 существуют два эквивалентных представления рационального числа, и при решении ряда задач необходимо уметь переводить рациональное число из одного представления в другое и наоборот. Делением непосредственно («уголком») числителя обыкновенной дроби на её знаменатель всегда можно представить дробь либо в виде конечной десятичной дроби (если простыми множителями знаменателя являются только двойки и пятерки), либо в виде бесконечной десятичной периодической дроби (в остальных случаях).
Сформулируем и докажем удобное на практике обратное правило перевода -периодической десятичной дроби в обыкновенную дробь.
Теорема 2. Чтобы перевести периодическую дробь в обыкновенную, надо из числа, стоящего до второго периода, вычесть число, стоящее до первого периода, и сделать эту разность числителем, а в знаменателе написать цифру 9 столько раз, сколько цифр в периоде, и после девяток дописать столько нулей, сколько цифр между запятой и первым периодом.
Доказательство. Пусть дано число в виде десятичной периодической дроби
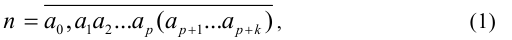
где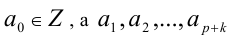 
— цифры. Необходимо доказать, что
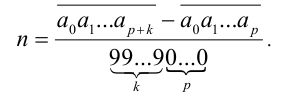
Умножим равенство (1) на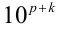 
(это равносильно переносу десятичной запятой на р + к позиций вправо):
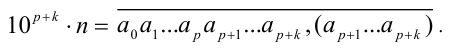
Умножим теперь равенство (1) на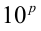 
(это равносильно переносу десятичной запятой на р позиций вправо):
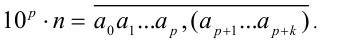
Вычтем друг из друга последние два равенства и воспользуемся тем, что периоды у чисел, стоящих в правых частях равенств, оказались одинаковы и поэтому при вычитании взаимно уничтожатся:
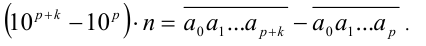
Выражая отсюда n , получаем искомый результат
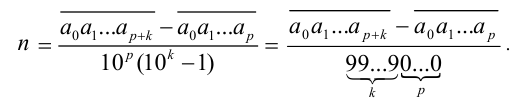
Замечание. После этого останется только привести полученную обыкновенную дробь к несократимому виду (если она оказалась сократимой). Рассмотрим несколько примеров.
Пример №73.
Упростить рациональное число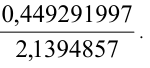 
Решение:
Домножая числитель и знаменатель дроби на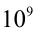 
получим
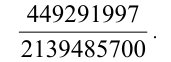
Далее «столбиком» аккуратно поделим числитель на знаменатель:
Пример №74.
Перевести периодическую дробь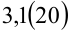 
в обыкновенную.
Решение:
Воспользовавшись данным правилом, сразу получим
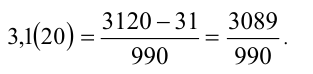
Если же повторить весь процесс вывода формулы для данного примера, то это будет выглядеть следующим образом. Обозначим переводимое число через x , затем умножим равенство x = 3,1 (20) на 10:
После этого ещё раз умножим равенство x = 3,1(20), но уже на 1000 и получим
Если теперь вычесть из равенства (3) равенство (2), то одинаковые периоды у чисел в правых частях равенств взаимно уничтожатся, и получим 990х = 3089, откуда и находим искомое представление числа x в виде обыкновенной дроби.
Ответ: 3,1(20) = 3089/990 .
Другой, более стандартный, но менее «короткий» способ перевода основан на использовании свойства суммы всех членов бесконечно убывающей геометрической прогрессии. Рассмотрим пример с той же периодической дробью 3,1(20).
Выполним следующую цепочку преобразований:
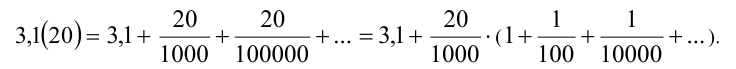
Заметим, что в скобках находится сумма всех членов бесконечно убывающей геометрической прогрессии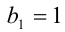 
и знаменателем 
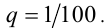Применяя известную формулу 
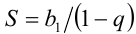, упрощаем выражение в скобках. Далее остаётся привести всё к виду одной дроби и, возможно, сократить её:
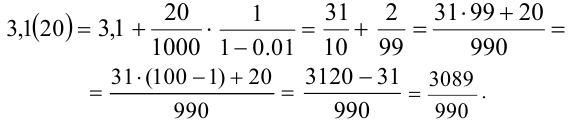
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
