Оглавление:
Правила дифференцирования и таблица производных элементарных функций разработана на основе определения производной (5.1), приёмов и правил вычисления пределов.
Так, если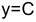 
(
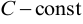), то для любого 
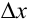приращение функции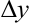 
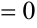, следовательно
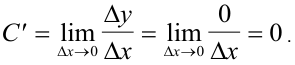
В этом состоит первое правило дифференцирования. Укажем остальные правила.
Правила дифференцирования функций
1. Производная постоянной величины равна нулю
2. Производная аргумента равна единице. Так, если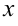 
— аргумент, то
3. Производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
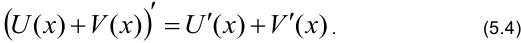
4. Производная произведения двух функций
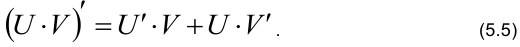
5. Постоянный множитель выносится за знак производной.
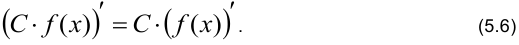
6. Производная частного двух функций.
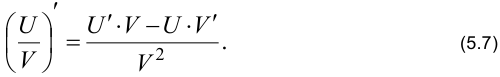
7. Производная сложной функции. Пусть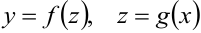 
. Множество всех 
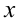, при которых значения 
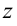входят в область определения функции 
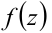является областью определения сложной функции 
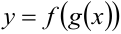. При этом 
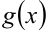называется внутренней функцией, функция 
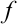называется внешней функцией.
Если функция 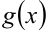имеет производную в точке 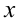, а функция 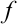имеет производную в точке 
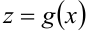, то сложная функция у имеет производную, равную произведению производной от внешней функции на производную от внутренней функции
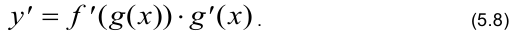
Пример:
Сложная функция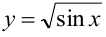 
. Здесь корень — внешняя, а
синус — внутренняя функции. Если обозначить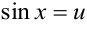 
, то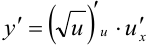 
, поэтому 
.
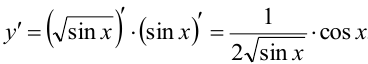Таблица 2 — Производные основных элементарных функций
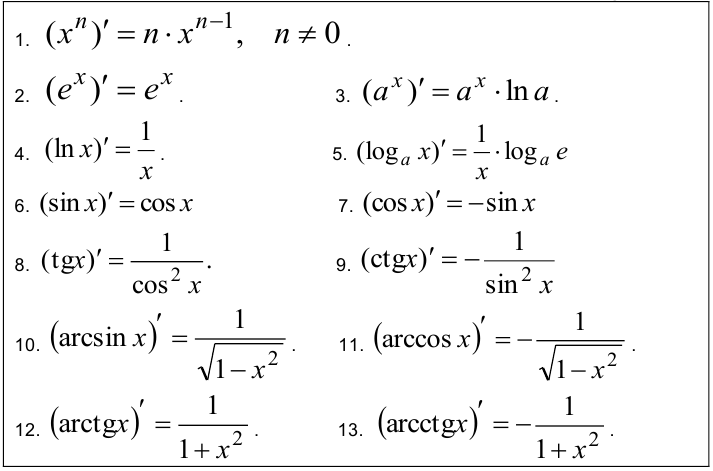
Пункт 1-й таблицы производных имеет несколько важных частных случаев:
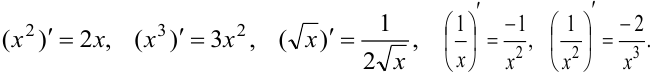
Пример:
а)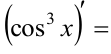 
(пункт 1 таблицы)
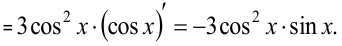
б)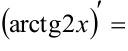 
(пункт 12 таблицы)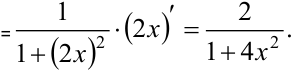 
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
