Правила дифференцирования функции

Нахождение производной функции непосредственно по определению занимает много времени и часто связано с большими трудностями. Поэтому на практике применяют следующие правила дифференцирования:

Пусть 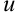и 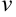— дифференцируемые функции, 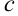— константа. Тогда справедливы правила нахождения производной суммы, произведения и частного двух функций:

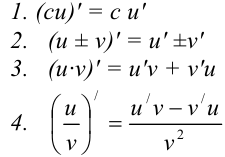
Рассмотрим примеры нахождения производных функций с использованием правил дифференцирования:

Пример №11.2.

Найдите производную функции .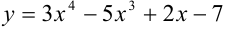

Решение:

Функция представляет собой сумму и разность выражений. Тогда для нахождения её производной воспользуемся правилом :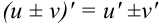

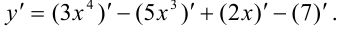
Константу можно вынести за знак производной по правилу: 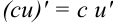. Тогда

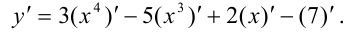
Далее воспользуемся формулами нахождения производных:

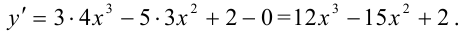
Ответ: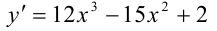

Пример №11.3.

Найдите производную функции 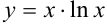в точке .

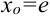Решение:

Найдем производную функции 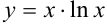как производную произведения. Воспользуемся правилом :

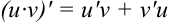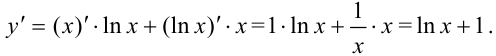
Для нахождения производной функции в точке в производную 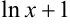подставим 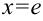. Тогда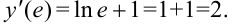

Ответ: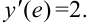

Пример №11.4.

Найдите производную функции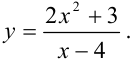

Решение:

Функция представляет собой дробь. Тогда для нахождения её производной воспользуемся правилом :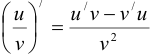

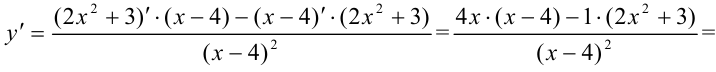
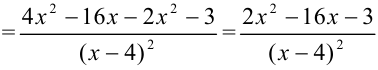
Ответ: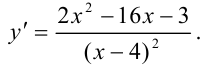

Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:

Предмет высшая математика

Другие лекции по высшей математике, возможно вам пригодятся:

Понятие производной функции.

Нахождение производных основных элементарных функций.

Производная сложной функции.

Геометрический смысл производной.