Оглавление:

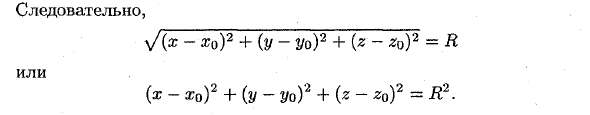



Поверхности и линии в пространстве и их уравнения
- ПОВЕРХНОСТИ И ЛИНИИ В ПРОСТРАНСТВЕ И ИХ УРАВНЕНИЯ 1. Поверхность и ее уравнение. Поверхность в пространстве можно рассматривать как геометрическое место точек, удовлетворяющих какому-либо условию. Например, сфера радиуса R с центром в точке 0 \ есть геометрическое место всех точек пространства, находящихся от точки 0 \ на расстоянии R. Прямоугольная система координат Oxyz в пространстве позволяет установить взаимно однозначное соответствие между точками пространства и тройками чисел х, у и г -. Их координаты Свойства, общая все точки поверхности, можно записать в виде уравнения, связывающая координата всех точек поверхности.
которому удовлетворяют координаты каждой точки, лежащей на поверхности, и не удовлетворяют координаты точек, не лежащих на этой Поверхностные координаты, точки и z в уравнении Уравнение поверхности позволяет изучение геометрических свойств поверхности заменить исследованием его уравнения.
Уравнением данной поверхности в прямоугольной системе координат Oxyz называется такое уравнение Р (х, у, г) = 0 с тремя переменными х, у и г, Людмила Фирмаль
Так, для того, чтобы узнать, лежит ли точка М \ {х ] у \ г%) на данной поверхности, достаточно подставить координаты точки М \ в уравнение поверхности вместо переменных если точка находится на поверхности, если не удовлетворительно . Пример: Найдет уравнение сферы радиуса R с центром в точке 0 \ (хо \ уо \ за) Согласно определению сферы расстояния любой ее точки М (ж, у, г) от центра 0 \ (жр; уры; ZQ) равно радиус Л , т. е. OiM = R. Но ОхМ = \ OiM \, где OiM = (х-х0 \ у-у0 \ z- z0). Следовательно, у / (х-х0) 2 + (у-Уо) 2 + (z- z0) 2-Я ИЛИ (х-гг0) 2 + (2 / -Уо) 2 + (z-z0) 2 = # 2.
И не удовлетворяю Если центр сферы 0 \ соответствует точке начала координат, то уравнение сферы принимает вид х2 -4у2 4-2 -4у Если такое же дано уравнение вида F (x; у; z) = 0, то оно, вообще говоря, определяется в пространскопне Выражение «вообще говоря» означает, что в отдельных случаях уравнение F (х \ у \ г) = 0 может определять не поверхность, а точку, линию или вовсе не определять никакой геометрический образ.
| Парабола | Различные виды уравнений плоскости в пространстве |
| Общее уравнение линий второго порядка | Плоскость. Основные задачи |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Говорят, «поверхность вырождается». . Так, уравнению 2х2 + у1 4- z2 4-1 = 0 не удовлетворяют никакие действительные значения гг, у, г Уравнению 0 • х2 4- у2 + z2 = 0 удовлетворяют лишь координаты точек, лежащих на оси Ох (из уравнения следует: 2 / = 0, z = 0, а ж-любое число). Итак, поверхность в пространстве может быть геометрической и аналитической. 1. Уравнение этой поверхности. 2. Дано уравнение F (x \ y \ z) = 0. Исследовать форму поверхности, определяемой этим уравнением.
Уравнения линии в пространстве Fx (x-y \ z) = b F2 (x; y} z) = 0 Геометрия и геометрия Fx (x \ y \ z) = 0, F3 (®; y; *) = 0.Уравнение системы (1) 1-2 = 0
Если Fi (х] у] г) = 0 и Р2 {х \ у \ г) ~ = О — уравнения двух поверхностей, определяющих линию L, то координаты точек этой линии удовлетворяют системе двух уравнений с тремя неизвестными Людмила Фирмаль
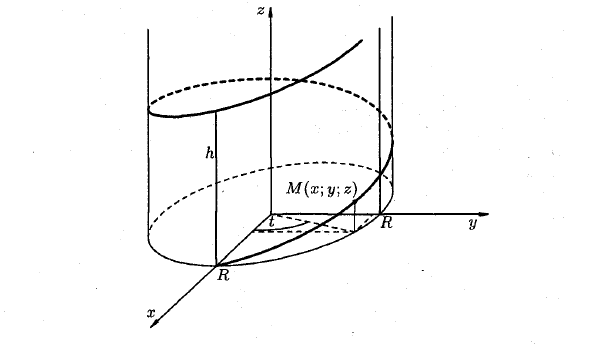
Траектории движения точки. (2) M (x \ y \ z) f = r (t) или параметрическими уравнениями х = х (т), У = 2 / (*), г = z (т) проекциями (2) на оси координат. Например, параметрические уравнения х = Я стоимость, у-R sin t, * = Если точка М равномерно двигается по образующей круговой цилиндру, а сам цилиндр равномерно вращается вокруг оси, то точка М описывает винтовая линия.

