Поверхности и линии уровня
Рассмотрим скалярное поле, задаваемое функцией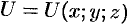 
. Для наглядного представления скалярного поля используют поверхности и линии уровня.
Поверхностью уровня скалярного поля называется геометрическое место точек, в которых функция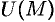 
принимает постоянное значение, т. е.
Давая в уравнении (70.1) величине с различные значения, получим различные поверхности уровня, которые в совокупности как бы расслаивают поле. Через каждую точку поля проходит только одна поверхность уровня. Ее уравнение можно найти путем подстановки координат точки в уравнение (70.1).
Для скалярного поля, образованного функцией
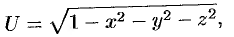
поверхностями уровня является множество концентрических сфер с центрами в начале координат: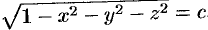 
. В частности, при 
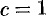получим 
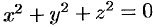, т. е. сфера стягивается в точку.
Для равномерно раскаленной нити поверхности уровня температурного поля (изотермические поверхности) представляют собой, круговые цилиндры, общей осью которых служит нить.
В случае плоского поля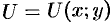 
равенство 
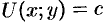представляет собой уравнение линии уровня поля, т. е. линия уровня — это линия на плоскости 
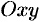, в точках которой функция 
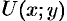сохраняет постоянное значение.
В метеорологии, например, сети изобар и изотерм (линии одинаковых средних давлений и одинаковых средних температур) являются линиями уровня и представляют собой функции координат точек местности.
Линии уровня применяются в математике при исследовании поверхностей методом сечений (см. п. 12.9).
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Периодические функции. Периодические процессы |
| Разложение в ряд фурье периодических функций с периодом 2п |
| Производная по направлению скалярного поля |
| Векторные линии поля |
