Оглавление:








Поведение сечений вблизи порога реакции
- Секция возле порога реакции Общая внутренняя энергия продукта реакции Если это решение одинаково для исходных частиц, реакция Рог: Кинетическая энергия E Столкновение частиц (в системе инерционных центров) У Ei есть определенные пороги. Думать о природе Энергетическая зависимость сечения реакции вблизи порога.
- В этом случае в результате реакции Опять только две частицы (тип A + B = A ‘+ B’ реакция). Относительная скорость образовавшегося чаа близка к порогу v ‘ Палка маленькая. Эта реакция Реакции, при которых воздействующие частицы являются медленными. для Поэтому зависимость сечения от vf легко найти Используя принцип известного детального равновесия (144.13).
Энергетическая зависимость реакций с ВФ Скорость входного канала (§143). Людмила Фирмаль
Широкая категория Реакция при отсутствии кулоновского взаимодействия между частицами A и B Действия (например, ядерные реакции, включающие образование ядерных реакций) Медленные нейтроны), поэтому сечение Реакция пропорциональна г / 2 (1 / г /). cg oo v1. (147,1) Поэтому энергетическая зависимость площади поперечного сечения выглядит следующим образом.
Количество частиц для раскачивания: отношение г / и сечение реакции с ним Он пропорционален корню разницы E-Ei. ar = A l / E-Ep. (147,2) Амплитуды рассеяния разных каналов связаны С другими унифицированными отношениями. Благодаря этой связи Когда вы открываете новый канал, Зависимость энергетической зависимости от сечения Процессы, включающие упругое рассеяние (Э. Вигнер, 1948; А. И. Баз, 1957; Г. Брайт, 1957).
Выяснить происхождение, Природа этого явления рассматривает простейший случай Ниже порога реакции возможно только упругое рассеяние. Вблизи порога частицы A ‘и B’ образуются в оп-состоянии. Битовый момент I = 0 (это в точности соответствует закону (147,2)). Если частицы, участвующие в реакции, не имеют вращения, Так как орбитальный импульс сохраняется, система частиц A + B также в 5 штатах.
(142.7) Согласно части Различные сечения реакции с I = 0 связаны с элементами матрицы S ‘. Формула, соответствующая упругому рассеянию 4 0) = J (1- | So | 2), (147,3) Где k — волновой вектор сталкивающихся частиц. уравнивание (147.2) и (147.3), превышающие порог реакции, He, модуль \ Sq \ order y / до значения E-En 50 | = 1-f-Au / E-Eu, E> Eu, (147,4) Z7t Где ki = y / 2mEi / H, где m — приведенная масса частиц A и B. в
Поскольку область ниже порога является только упругим рассеянием, \ S0 \ = 1, E Ay / E ~ En), (147,6) 5o является константой (если E <Ei, корень y / E-Ei Модуль выражений в мнимых числах и скобках (Только единицы с меньшим значением). Для всех IΦ0 неупругого рассеяния нет, поэтому St = e2iSl, I f 0, (147,7) Кроме того, в области, близкой к порогу фазы, Значение 1 при Е = Еи).
Подставляя полученное значение Si в формулу (142.2), Следующее уравнение для амплитуды рассеяния вблизи порога: Где / n (0) — амплитуда рассеяния при E = Eu. Отличается от здесь Потенциальное сечение рассеяния ^ = | / n (0) | 2 + ^ A y / E-En I m {f n (e) e ~ 2iSo} для E> En, Около 2 тг = \ W) \ 2-> Ay / E-En Re {f n (e) e-2iSo} для E ) ‘1 I E n и E < <E, и они разлагаются по степени разности E-E n. рассеяние: (e2r5 ° -1) / (2rcp).
В результате завершено Сечение упругого рассеяния вблизи порога выражается следующим образом. Nie: , Пр «(147.10) [sin <co делает для E <Ei. Эта зависимость принимает форму рисунка а или б. 50 каждый Положительный или отрицательный знак, потому что грех Таким образом, наличие порога реакции Появление характерных особенностей энергетической зависимости Мост сечения упругого рассеяния.
Состояние на складе Изменение спина частиц, конечно, количество Формула общая 1) остается прежним. Ниже порога С упругим рассеянием И другие реакции имеют сходные функции Отображается в разделе. У них всех есть E = близлежащая функция Ep Корневая линейная функция y / \ E-Eu \ c Различные склоны выше и ниже порога.
Ядерная реакция с взлетом Заряженные частицы Чай, продукты реакции (чай Столица A ‘l B’) Кулоновская сила оттаяла Киваешь. В этом случае сечение реакции vf-Y 0 (т.е. E-y Ei) в геометрической прогрессии Перейти к нулю для всех продуктов Нет функции с энергией воды Другие разделы процесса не встречаются. И, наконец, 2 низких медленных зарядки напротив частицы между си Обращение Ли Кулона.
Такой передел Акции, связанные детальными принципами равенства Этот участок с обратным сечением реакции (143,6) Две части, которые тянут медленно каллиграфов Грузии. Таким образом, для v ‘-y 0, сечение До определенного предела или = const при vf —y 0, (147,11) То есть, когда порог превышен, реакция происходит сразу с конечным поперечным сечением.
1) система частиц s-состояния A ‘+ B g для ненулевого спина Потому что может быть полный момент, отличный от нуля, Различные орбитальные возможности для системы A + B Ответственный за характер функции поблизости Углом такой реакции является сечение упругого рассеяния (А. И. Баз, 1959). Однако это не может быть сделано напрямую известным способом.
- Подпороговый метод (147.11) простым способом Используется для вышеуказанных незаряженных частиц. По сравнению с последним случаем ситуация осложняется ими Теперь система частиц A ‘+ B’ Lopologo регион (E bG, Где u = y / 2m (ET1-E) / K). При этом должно быть ниже порога be \ Saa \ = 1, что приводит к линейной дробной функции Саа (ты похож Saa = (147,12) Где r] — действительное число, а / 3 — комплексная константа.
Определить величину A как функцию импульса kb. с того времени Между частицами, уже находящимися в силе кулоновского притяжения, r ++ задается асимптотически кулоновской волновой функцией Это пропорционально бесконечности. В подвесном поле Чтобы нажать эту функцию, нажмите + iF $ плюс Go и Fq (138,4) и (138,7). Переход на привлекательное поле Это одновременное изменение знака k и r1).
Делая это 1) Используйте подвесной блок. Изменить знак к и г Соответствует изменению знака длины подвесного блока официально. Людмила Фирмаль
Подстановка и вычисление логарифмической производной (см. §138), get1) A = i- «P (3 Вт S) ~ + H-W- (147LZ) Где kb предполагается действительным числом, Формула относится к области, которая превышает порог. кд 0 за Четвертый член (147.13) имеет тенденцию исчезать при r, а второй член стремится к нулю (Примечание: см. Стр. 695).
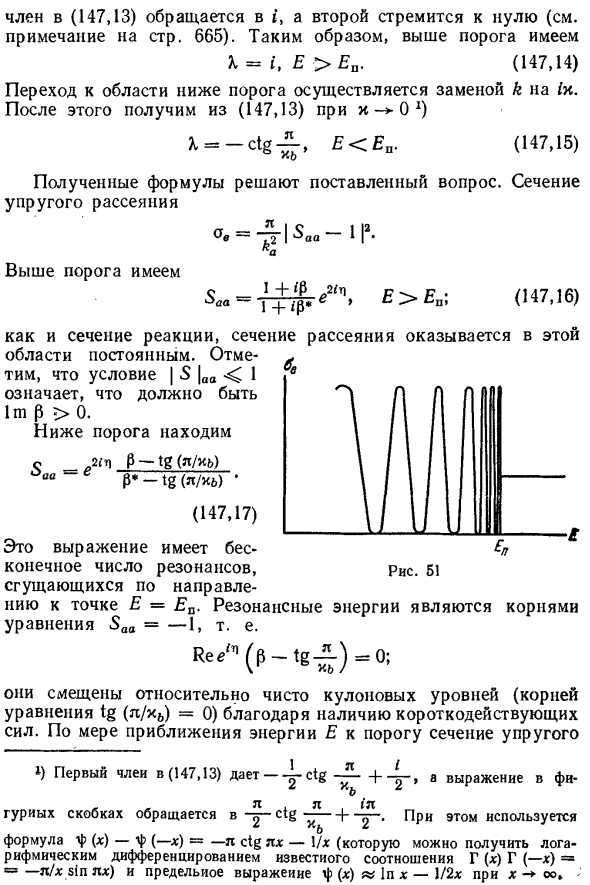
Поэтому, когда порог превышен A = r, E> E P. (147,14) Переходы в область ниже порогового значения выполняются путем замены k на gx. После этого получаем из (147.13) как x-) ►О2) A = -ctg-, E SJ Полученная формула решает поставленную проблему. Seche Упругое рассеяние ae = Saa ~ 1 | 2. к Превышен порог ^ E> E B; (147,16) 1 + гр Как и сечение реакции, сечение рассеяния отображается в этом Район постоянный.
Условие \ S \ aa ^ 1 есть Im / 3> должно быть 0. Ниже порога Saa = e2i ^ -tf * / * b) (147,17) / 3-т г (7 т / к б) Эта формула имеет бесчисленные резонансы и делает ее толще Двигайтесь к точке E = Ei. Резонансная энергия Является ли корень уравнения Saa = −1, т.е. Аренда ^ / 3-тг- ^ = 0;
г) фигурные скобки опущены, чтобы упростить дальнейшие выражения, В зависимости от k, действительная постоянная (-In 2go-2 (7), К незначительному переопределению сложного / 3 и реального Значение r] в (147.12). 2) Первое слагаемое в (147.13) дает — (1/2) ctg (7r / Kb) + r / 2 и φ В скобках (7Γ / 2) ctg (7r /> cf) + m / 2 Будет использоваться Формула φ (x) -φ (-x) = -7rctg7rx-1 / x (это лог
Производная ритма известного отношения Γ (x) Γ (—x) = = —7m / x simrx) и формула ограничения φ (x) In In x-1/2 / при x oo. Это чисто кулоновские уровни (корень Уравнение tan (7m / n) = 0) Наличие силы ближнего действия. по Приведите энергию E ближе к порогу Упругая рассеивающая вибрация Между нулем и Atg / k2, как показано 51. Общая ширина схематично на рисунке Подпороговая область Резонансная структура выявлена Первый зависит от количества энергии кулон 1-го уровня). Рисунок 5
Смотрите также:
| Формулы Брейта и Вигиера | Неупругие столкновения быстрых электронов с атомами |
| Взаимодействие в конечном состоянии при реакциях | Эффективное торможение |

