Оглавление:
Поток поля
Пусть векторное поле образовано вектором (71.1). Для наглядности будем считать 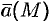 вектором скорости некоторого потока жидкости, движущейся стационарно. Представим, что некоторая поверхность
вектором скорости некоторого потока жидкости, движущейся стационарно. Представим, что некоторая поверхность  находится в этом потоке и пропускает жидкость. Подсчитаем, какое количество жидкости протекает через поверхность
находится в этом потоке и пропускает жидкость. Подсчитаем, какое количество жидкости протекает через поверхность  .
.
Выберем определенную сторону поверхности  . Пусть
. Пусть 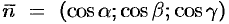 единичный вектор нормали к рассматриваемой стороне поверхности
единичный вектор нормали к рассматриваемой стороне поверхности  . Разобьем поверхность на элементарные площадки
. Разобьем поверхность на элементарные площадки 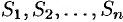 . Выберем в каждой площадке точку
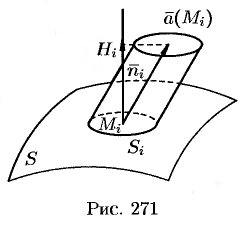
. Выберем в каждой площадке точку  (см. рис. 271) и вычислим значения вектора скорости
(см. рис. 271) и вычислим значения вектора скорости 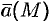 в каждой точке:
в каждой точке: 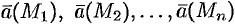 .
.
Будем приближенно считать каждую площадку плоской, а вектор  постоянным по модулю и одинаково направленным в каждой точке площадки. Тогда за единицу времени через
постоянным по модулю и одинаково направленным в каждой точке площадки. Тогда за единицу времени через 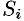 протекает количество жидкости, приближенно равное
протекает количество жидкости, приближенно равное 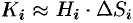 , где
, где 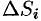 — площадь
— площадь 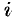 -й площадки,
-й площадки, 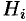 — высота
— высота 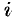 -го цилиндра с образующей
-го цилиндра с образующей 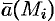 . Но
. Но 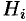 является проекцией вектора
является проекцией вектора 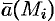 на нормаль
на нормаль 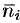 :
: 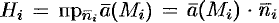 , где
, где 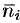 — единичный вектор нормали к поверхности в точке
— единичный вектор нормали к поверхности в точке 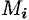 . Следовательно, общее количество жидкости, протекающее через всю поверхность
. Следовательно, общее количество жидкости, протекающее через всю поверхность  за единицу времени, найдем, вычислив сумму
за единицу времени, найдем, вычислив сумму
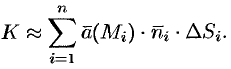
Точное значение искомого количества жидкости получим, взяв предел найденной суммы при неограниченном увеличении числа элементарных площадок и стремлении к нулю их размеров (диаметров 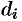 площадок):
площадок):
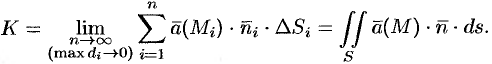
Независимо от физического смысла поля 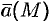 полученный интеграл называют потоком векторного поля.
полученный интеграл называют потоком векторного поля.
Потоком вектора  через поверхность
через поверхность  называется интеграл по поверхности от скалярного произведения вектора поля на единичный вектор нормали к поверхности, т. е.
называется интеграл по поверхности от скалярного произведения вектора поля на единичный вектор нормали к поверхности, т. е.

Рассмотрим различные формы записи потока вектора. Так как
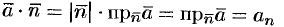
(см. (6.2)), то

где 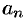 — проекция вектора
— проекция вектора  на направление нормали
на направление нормали 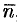 ,
, 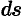 — дифференциал (элемент) площади поверхности.
— дифференциал (элемент) площади поверхности.
Иногда формулу (71.3) записывают в виде
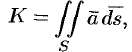
где вектор 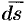 направлен по нормали к поверхности, причем
направлен по нормали к поверхности, причем 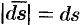 .
.
Так как 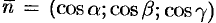 ,
, 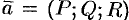 , где
, где 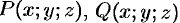 ,
, 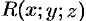 -— проекции вектора
-— проекции вектора  на соответствующие координатные оси, то поток (71.3) вектора
на соответствующие координатные оси, то поток (71.3) вектора  , можно записать в виде
, можно записать в виде
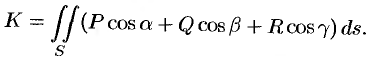
Используя взаимосвязь поверхностных интегралов I и II рода (см. формулу (58.8)), поток вектора можно записать как
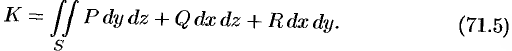
Отметим, что поток 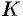 вектора
вектора  есть скалярная величина. Величина
есть скалярная величина. Величина 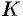 равна объему жидкости, которая протекает через поверхность
равна объему жидкости, которая протекает через поверхность  за единицу времени. В этом состоит физический смысл потока (независимо от физического смысла поля).
за единицу времени. В этом состоит физический смысл потока (независимо от физического смысла поля).
Особый интерес представляет случай, когда поверхность замкнута и ограничивает некоторый объем  . Тогда поток вектора записывается в виде
. Тогда поток вектора записывается в виде 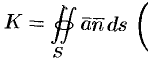 иногда
иногда 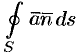 или
или 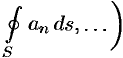 .
.
В этом случае за направление вектора 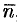 обычно берут направление внешней нормали и говорят о потоке изнутри поверхности
обычно берут направление внешней нормали и говорят о потоке изнутри поверхности  (см. рис. 272).
(см. рис. 272).
Если векторное поле 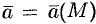 есть поле скоростей текущей жидкости, то величина потока
есть поле скоростей текущей жидкости, то величина потока 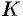 через замкнутую поверхность дает разность между количеством жидкости, вытекающей из области
через замкнутую поверхность дает разность между количеством жидкости, вытекающей из области  (объема
(объема  ) и втекающей в нее за единицу времени (в точках поверхности
) и втекающей в нее за единицу времени (в точках поверхности  , где векторные линии выходят из объема
, где векторные линии выходят из объема  , внешняя нормаль образует с вектором
, внешняя нормаль образует с вектором  острый угол и
острый угол и 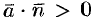 ; в точках, где векторные линии входят в объем,
; в точках, где векторные линии входят в объем, 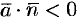 ).
).
При этом если 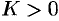 , то из области
, то из области  вытекает больше жидкости, чем в нее втекает. Это означает, что внутри области имеются дополнительные источники.
вытекает больше жидкости, чем в нее втекает. Это означает, что внутри области имеются дополнительные источники.
Если 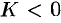 , то внутри области
, то внутри области  имеются стоки, поглощающие избыток жидкости.
имеются стоки, поглощающие избыток жидкости.
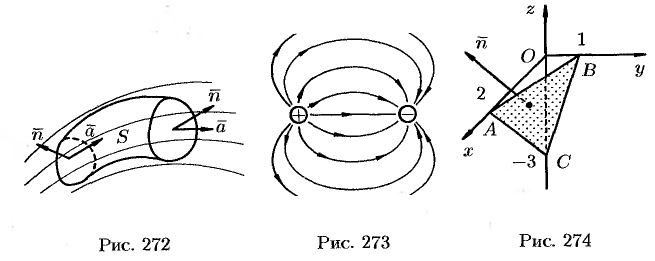
Можно сказать, что источники — точки, откуда векторные линии начинаются, а стоки — точки, где векторные линии кончаются. Так, в электростатическом поле источником является положительный заряд, стоком — отрицательный заряд магнита (см. рис. 273).
Если 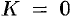 , то из области
, то из области  вытекает столько же жидкости, сколько в нее втекает в единицу времени; внутри области либо нет ни источников, ни стоков, либо они таковы, что их действие взаимно компенсируется.
вытекает столько же жидкости, сколько в нее втекает в единицу времени; внутри области либо нет ни источников, ни стоков, либо они таковы, что их действие взаимно компенсируется.
Пример №71.2.
Найти поток вектора 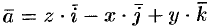 через верхнюю сторону треугольника, полученного при пересечении плоскости
через верхнюю сторону треугольника, полученного при пересечении плоскости 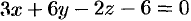 с координатными плоскостями (см. рис. 274).
с координатными плоскостями (см. рис. 274).
Решение:
Поток найдем методом проектирования на три координатные плоскости. Для этого воспользуемся формулой (71.5). В нашем случае 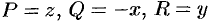 . Имеем:
. Имеем:
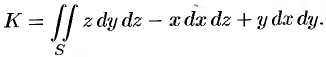
Расчленим этот поверхностный интеграл на три слагаемых, затем сведем их вычисление к вычислению двойных интегралов. Нормаль к верхней стороне треугольника образует с: осью  тупой угол, с осью
тупой угол, с осью 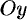 — тупой, а с осью
— тупой, а с осью 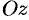 — острый угол. (Единичный вектор данной плоскости есть
— острый угол. (Единичный вектор данной плоскости есть 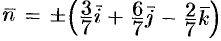 ; на верхней стороне
; на верхней стороне 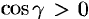 , поэтому надо выбрать знак «минус»; получим:
, поэтому надо выбрать знак «минус»; получим: 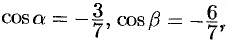
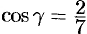 .)
.)
Итак, 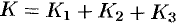 . Находим
. Находим 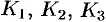 :
:
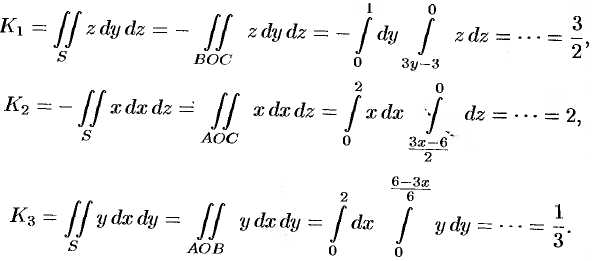
В результате имеем: 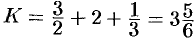 .
.
Дополнительный пример №71.3.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Производная по направлению скалярного поля |
| Векторные линии поля |
| Векторные дифференциальные операции первого порядка |
| Векторные дифференциальные операции второго порядка |

