Оглавление:


Потеря устойчивости за пределом упругости (продолжение)
- Потеря устойчивости за пределом упругости(продолжение). Изучение устойчивости сжатого стержня приводит к установлению некоторых соотношений между критическим напряжением и гибкостью. Пока напряжение меньше предела упругости, эта зависимость задается
формулой за пределом упругости(139.1)—по формуле (139.10) можно опубликовать формулировку полученной задачи.
Мы откладываем критическое напряжение на вертикальную ось, гибкость-на Людмила Фирмаль
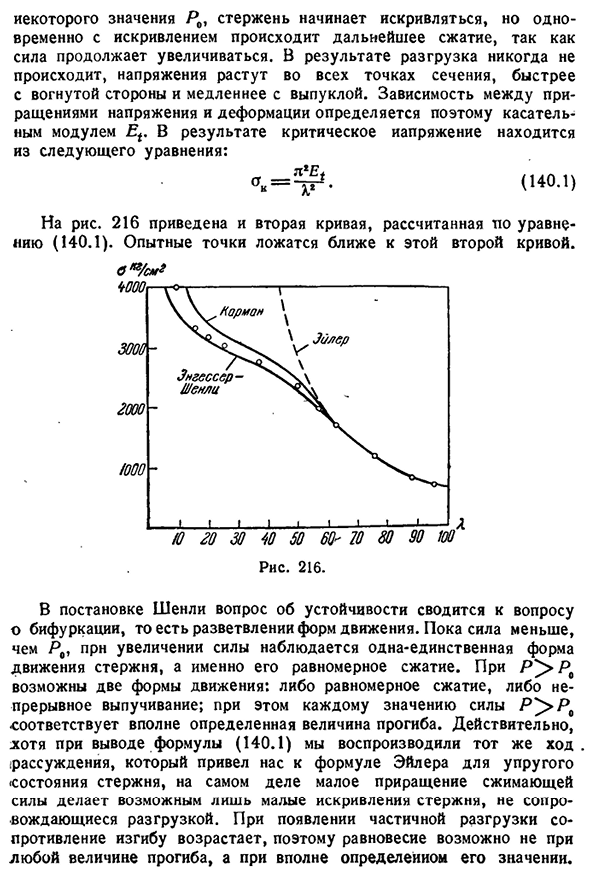
горизонтальную ось. Для напряжений, меньших предела упругости, уравнение (139.1) дает кривую гиперболического типа(рис. 216). Для напряжений, превышающих предел упругости, кривая строится
по уравнению (139.10). Чтобы построить точную диаграмму сжатия материала, используя эту кривую, полезно рассчитать гибкость данного участка с учетом различных значений сжимающего напряжения при построении приведенной кривой Моджи в зависимости от сжимающего напряжения. В первом исследовании Энгессера(1889) выражение критического напряжения отличалось от выражения(139.10) вместо приведенного модуля K, и в нем
- появился касательный модуль Et. Ф. С. Ясинский обратил внимание на возможность образования зон разгрузки с потерей устойчивости, после чего энгессер пересмотрел свою теорию и ввел данный
модуль К. представим, что стержень подвергается непрерывно возрастающей силе; когда сила достигает 312, получается устойчивость упругого и пластического равновесия. ДВЕНАДЦАТЫЙ При некоторых значениях Р » стержень начинает изгибаться, но в то же время с искривлением, по мере того как сила продолжает увеличиваться, происходит дальнейшее сжатие. В результате разгрузка не осуществляется, напряжение возрастает во всех точках сечения, оно быстрее на вогнутой стороне и медленнее
на выпуклой стороне. Поэтому зависимость между приращением напряжения Людмила Фирмаль
и деформации определяется касательным коэффициентом Et. В результате критическое напряжение получается из следующего уравнения: (140.1) Для риса. 216) и НИУ(140.1). Вторая кривая, вычисленная по уравнению, расположена ближе к этой второй кривой. В постановке Шенли проблема устойчивости сводится к проблеме бифуркации, то есть к бифуркации формы движения. Единственная форма движения полотна, т. е. его равномерное сжатие-РА больше, пока сила меньше, мощность ПРН увеличивается на единицу. При P > RA возможно либо равномерное сжатие, либо непрерывная выпуклость, поэтому каждое значение силы P~^>RA
соответствует прогибу значительной величины. Действительно, при выводе формулы (140.1) мы воспроизвели те же рассуждения, которые привели к формуле Эйлера для упругого состояния стержня, но на самом деле с появлением небольшой инкрементной частичной разгрузки сжимающей силы сопротивление изгибу возрастает, так что равновесие возможно не при любом значении прогиба, а при четко определенном значении.
Смотрите также:

