Оглавление:





Потеря устойчивости за пределом упругости
- Потеря устойчивости за пределом упругости. Формула для критической силы Эйлера(138.6) явно применяется только тогда, когда материал следует закону Гука. Однако может случиться так, что сила, определяемая формулой Эйлера, вызывает сжимающее напряжение материала за пределами пропорциональности. Это, в частности,
объясняет плохое совпадение с опытом, обнаруженным в ранних экспериментах по проверке теории устойчивости Эйлера. Чтобы определить пределы применимости формулы Эйлера, приведем несколько иную форму. Для этого разделите обе части
уравнения (138.6) на площадь поперечного сечения стержня F ia. Слева Людмила Фирмаль
вы получаете критическое напряжение прибл. Это значение равно квадрату инерционного радиуса i секции (см.§ 110).Упругое и пластическое равновесие [CH, 308 стабильность. ХН Введем безразмерную величину а называемую гибкостью стержня: В — Выражение Эйлера переписывается следующим образом: =(139.1) Для длинных и тонких стержней а велико, следовательно, критическое
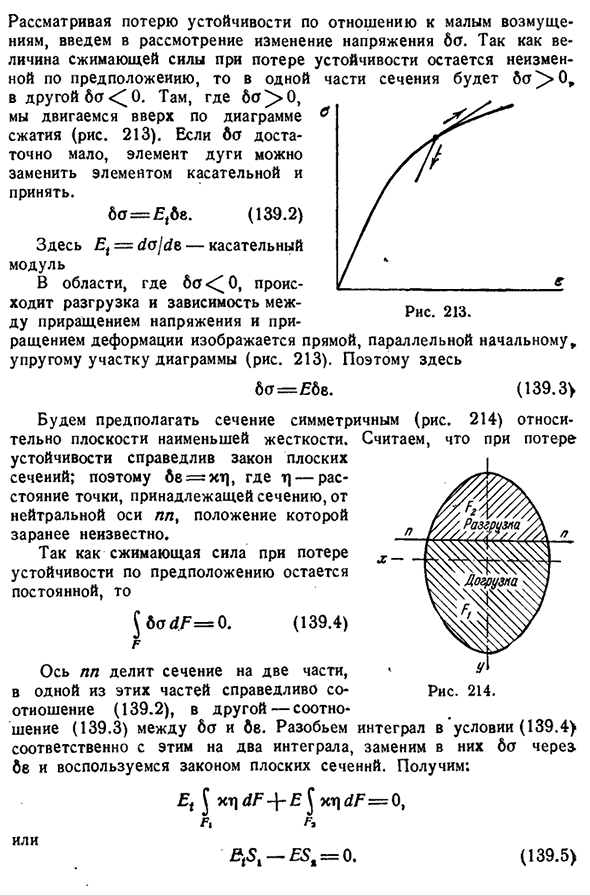
давление невелико. Ограничением применения формулы (139.1) является случай, когда Изменение напряжения Бо вводится с учетом потери устойчивости при малых возмущениях. Так как величина силы сжатия при потере устойчивости остается неизменной в предположении, то при любом другом b o<^0. Где Bo^>0,
- мы перемещаем фигуру сжатия вверх(рис. 213). Если Бо достаточно мал, замените его. Элемент дуги является касательным элементом, b o=E46E.(139.2)Et=do i da-касательный элемент Часть раздела будет Bo^>0. Здесь зависимость между модулем упругости в области разгрузки Bo0 и приращением напряжения и приращением деформации рисуется в виде прямой линии, параллельной начальной упругой части рисунка 213). 4Б о=е б е здесь.
ельно плоскости минимальной жесткости, устойчивости действует закон плоского поперечного сечения; следовательно, be = HT], где t] — расстояние точки, принадлежащей сечению, от нейтральной оси ll, положения А так как сжимающая сила потери устойчивости принимается постоянной Дж Б О Д Е=0. Ф Для любой из этих частей отношение(139.2) истинно, а для другой-отношение Bo быть (139.3). Мы разделяем интегралы в терминах (139.4) на два интеграла соответственно и заменяем Бо, используя закон плоского поперечного сечения, когда речь заходит о них. Вам; Эт от J ХТ]ДФ е НТ]
Д Ф=О, И=•>/ Мы считаем это в убыток Или (139.4) — Есть=0. (139.5) упругое Людмила Фирмаль
и пластическое равновесие [глава 310 стабильность. ДВЕНАДЦАТЫЙ Где 5 и 5-статические моменты области F и Ft относительно оси PP (оба считаются положительными). Здесь мы вычисляем момент относительно оси PP и по дополнительному напряжению BA: b/I= = j = DF=x[EtJt£/.]. (139.6) Ф Здесь и J, — момент инерции области Fx и Ft относительно оси PP. Уравнение(139.6) описывает зависимость между изгибающим моментом и кривизной. В упругой области эта зависимость задается следующими соотношениями:?>М=EJxk.
■(139.7), где E-модуль упругости, а Jx-момент инерции относительно центральной оси X. Рис, 215. В / Л л п ( / < ) />■ Но * Она выглядела как выше, а именно: bM-KJxn. (139.8)величина K называется уменьшенным временным или карманным коэффициентом, здесь (139.9) Как видите, данный модуль зависит не только от материала, но и от раздела. Теперь можно рассматривать как И потеря устойчивости от поперечной формы сжатого стержня точно такая же, как потеря устойчивости в упругой области(§ 136). В дифференциальном уравнении изгиба(136.1) оно получается на основе соотношения между моментом и кривизной (139.7),
и в соответствии с (139.8), в результате чего модуль упругости е вычисляется по карману К. необходимо заменить на модуль упругости: (139.10) Величина Et зависит от положения точки ia на диаграмме сжатия и, следовательно, от напряжения приблизительно. Это значение является результатом решения уравнения (139.10). Вычислите высоту h и ширину ft (L ’ S ft), уменьшенный модуль для прямоугольных сечений. Высота зоны загрузки 1L, высота зоны разгрузки (1 -|) L(фиг. 215). Тогда с=4г * ф т*. Ст=|(l_g)’футов».§ 140] потеря устойчивости сверх предела упругости
(продолжение) 311 Подставляя эти выражения в выражение (139.5), получаем следующее выражение: Таким образом, следующее: Г » Et_(Д-З Е=0. Один. Момент инерции всего сечения относительно оси X равен моменту инерции сечения относительно оси BH’jw, оси ll Л’ * ’*3zбыл> ——— з По формуле (139.9)модуль кармана т ф=4[(Л-Г)’+^’]Е. Если вы назначаете значение здесь, это выглядит так:
Смотрите также:

