Потенциальная энергия

Потенциальная энергия

Часть пространства, в которой на помещенную туда материальную точку действует сила, зависящая от места положения точки, называется силовым полем.

Причем, эта сила определяется с помощью силовой функции

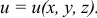
Если эта функция не зависит от времени, то такое поле называется стационарным. Если во всех точках она одинакова, то поле — однородное.

Если же проекции силы на декартовы оси есть частные производные от силовой функции по соответствующим координатам

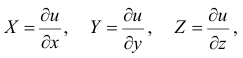
то такое поле называется потенциальным.

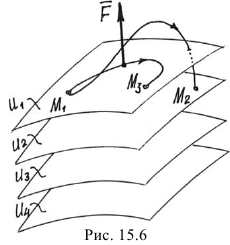
Вычислим работу силы потенциального поля при перемещении точки из положения 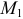в положение 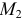(рис. 15.6).

Элементарная работа по выражению (15.4)

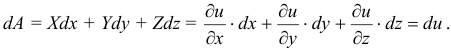
Это есть полный дифференциал силовой функции.

Работа на конечном перемещении

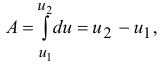
где 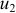и 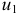— значения силовой функции в точках 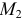и .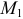

Следовательно, работа силы потенциального поля не зависит от траектории движения точки, а определяется лишь значениями силовой функции в начальном и конечном положениях точки.

Естественно, если точка вернется в начальное положение, работа силы 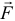будет равна нулю. Работа окажется равной нулю и при переходе в другую точку 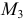, если там значение силовой функции будет такое же, как и в начальном положении.

Нетрудно догадаться, что точки с одинаковыми значениями силовой функции будут образовывать целую поверхность. И что силовое поле — это «слоёное пространство», состоящее из таких поверхностей (см. рис. 15.6). Эти поверхности называются поверхностями уровня, или эквипотенциальными поверхностями. Уравнения их: 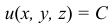( 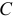— постоянная, равная значению 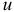в точках этой поверхности). А силовую функцию называют соответственно потенциалом поля.

Конечно, эквипотенциальные поверхности не пересекаются. Иначе существовали бы точки поля с неопределенным потенциалом. Поскольку при перемещении точки по эквипотенциальной поверхности работа силы 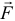равна нулю, то вектор силы перпендикулярен поверхности.

Выберем среди этих поверхностей какую-нибудь одну и назовем ее нулевой поверхностью (положим у нее ).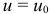

Работа, которую совершит сила 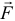при переходе материальной точки из определенного места 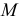на нулевую поверхность, называют потенциальной энергией 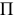точки в этом определенном месте 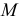. Следовательно,

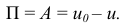
Заметим, что потенциальная энергия в одной и той же точке поля зависит от выбора нулевой поверхности. По формуле (15.13) силовая функция 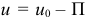. Поэтому проекции силы на декартовы оси, по (15.11), так как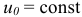

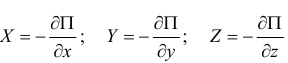
и вектор силы

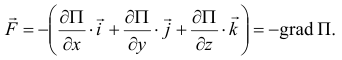
Рассмотрим несколько потенциальных полей.

Поле силы тяжести

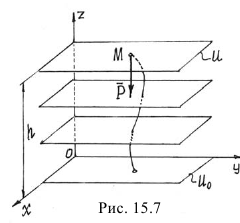
Вблизи поверхности Земли сила тяжести во всех точках одинакова 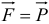, равна весу тела. Значит, это силовое поле однородное. Так как при перемещении точки в горизонтальной плоскости работа силы равна нулю, то эквипотенциальными поверхностями будут горизонтальные плоскости (рис. 15.7), а уравнения их: .

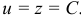Если нулевой поверхностью назначить плоскость 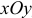, то потенциальная энергия точки в положении 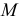будет равна работе силы тяжести (15.5):

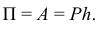
Поле упругой силы

При деформации упругого тела, например пружины, появляется сила (см. пример 15.3). То есть около этого тела возникает силовое поле, силы которого пропорциональны деформации тела и направлены в сторону недеформированного состояния. У пружины — в точку 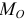где находится конец недеформированной пружины (рис. 15.8).

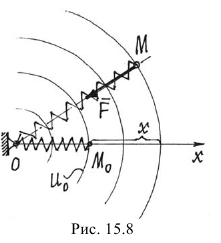
Если перемещать конец пружины так, чтобы длина ее не изменялась, то работа упругой силы 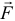будет равна нулю. Значит, эквипотенциальными поверхностями являются сферические поверхности с центром в точке .

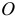Назначим нулевой поверхностью сферу, проходящую через точку 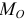через конец недеформированной пружины. Тогда потенциальная энергия пружины в положении её конца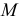 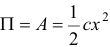по формуле (15.10).

При таком выборе нулевой поверхности потенциальная энергия всегда будет положительной 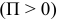и в растянутом, и в сжатом состояниях.

Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:

Помощь по теоретической механике

Кстати возможно вам будут полезны эти страницы:

Моменты инерции тел в теоретической механике

Работа силы в материальной системы

Кинетическая энергия

Теорема об изменении кинетической энергии материальной системы