Оглавление:



Потенциальная энергия растяжении
- Потенциальная энергия напряжения. Упругое тело, будучи деформированным, является аккумулятором энергии, которая тратится на деформацию. При устранении силы действия эта энергия отдается упругим телом того или иного вида.
Применение упругих аккумуляторов энергии широко распространено и применяется в конструкции часовых механизмов, таких как часы, некоторые записывающие устройства. В общем случае внешние силы приложены к упругому телу, с одной стороны, к сообщению скорости относительно частиц тела, то есть к кинетической энергии
т, с другой стороны, в виде потенциальной энергии деформации. Людмила Фирмаль
Уравнение энергетического баланса A=T — \ — U. (28.1) 60 напряжение-сжатие (Глава II Величина U представляет собой часть работы, затраченной на деформацию тела, и если тело упругое, то оно остается в нем до тех пор, пока не изменится нагрузка. Чтобы вычислить величину U, мы должны предположить, что внешняя сила приложена так, что кинетическая энергия T равна нулю.
Только в этом случае считается, что внутренние силы упругости между каждым моментом процесса уравновешиваются внешними силами, так как сила Р прикладывается не сразу, а постепенно, то есть медленно возрастая от нуля до максимума, скорость деформации практически не существует.、: А = У.
- Процесс деформации представляет собой последовательность бесконечно малых приращений удлинения d (l), вызванных ростом силы P, однозначно связанной с удлинением по закону крюка при растяжении и сжатии (28,2%).) Приращение D (A/) удлинения соответствует основной работе: д А-П Д (Л). При консолидации от D/=0 до конечного значения D/: м т/=J р д(а/). (28.3) Отчет Если вы замените его здесь: Сила-это выражение в соответствии с законом крюка (28.2), EF (M) 1 Двадцать одни (28.4)
Приведем две эквивалентные формы, записывающие выражение потенциальной энергии растяжения: Радиочастотный 2.’ (28.5) И= / RD/. (28.6) Если вы используете формулы (28.5) и (28.6), вам нужно помнить, что P является внешней силой только тогда, когда стержень неподвижен. В динамической материи сила, которая растягивает стержень, является, вообще говоря, суммой внешних сил и силы инерции. Эта сумма отображается в формулах (28.5) и (28.6).§ 29]Вы можете ударить напряжение 61
Энергию упругой деформации растяжения-сжатия удобно отнести к единице объема стержня. Это значение выражается как: В Отчет (28.7) Людмила Фирмаль
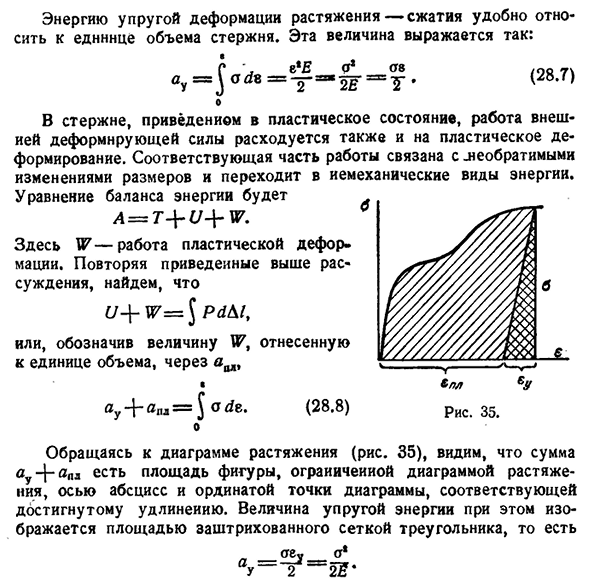
В стержне, приведенном в пластическое состояние, работа внешних деформирующих сил также расходуется на пластическую деформацию. Соответствующая часть работы связана с этим. Необратимые изменения размеров и переход к механической энергии. Уравнение энергетического баланса имеет вид A=T — \ — U — {~W. Здесь W-работа пластической деформации. Если вы повторите вышеприведенные рассуждения, U — \ — W=J P d M , Или, через ам, называют единицу объема, обозначающую величину W, Yau+d n l=$ode. Около (28.8) Смотрите диаграмму растяжения. 35), мы видим, что сумма au 4 ″ d PL — это площадь граничной фигуры по диаграмме расширения, оси абсцисс и вертикальной оси фигуры, соответствующей достигнутому удлинению. Величина упругой энергии представлена площадью треугольника, затененного сеткой.
Смотрите также:
| Расчет статически неопределимых систем по допускаемым нагрузкам | Напряжения при ударе |
| Остаточные напряжения после пластической деформации | Распространение упругих волн в стержнях |

