Поступательное движение
Поступательным движением твердого тела называется такое движение, при котором всякая прямая, неизменно связанная с этим телом, движется, оставаясь параллельной своему начальному положению.
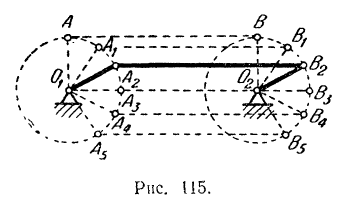
Примерами поступательного движения тела могут служить: движение кузова автомашины, движущейся по прямолинейному пути, движение поршня двигателя и т. д. Неправильно, однако, думать, что при поступательном движении тела траектории его точек должны быть непременно прямыми линиями. Так, например, спарник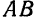 
(рис. 115), соединяющий кривошипы 
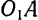и 
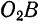двух
осе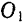й 
и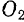 
, совершает поступательное движение, хотя его точки по отношению к корпусу паровоза и будут двигаться по окружностям. В самом деле, при вращении кривошипов 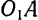и 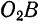вокруг их осе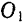й и 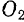положение спарника 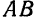будет изменяться. Но при равенстве длин кривошипов и при длине спарника, равной расстоянию между осями 
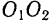, четырехугольник 
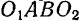будет всегда оставаться параллелограммом, следовательно, спарник 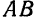всегда параллелен основанию 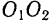, т. е. он движется, оставаясь параллельным своему начальному положению. В то же время точк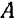и 
и 
спарника, а следовательно, и все остальные его точки по отношению к корпусу паровоза движутся по окружностям, радиус которых равен длине кривошипа.
Траекториями точек тела при его поступательном движении могут быть какие угодно кривые.
Заметим также, что термин «поступательное движение» применим только к движению тела, но не к движению одной точки. Понятие «движется, оставаясь параллельной своему начальному положению» никак не применимо к точке, не имеющей размеров.
Теорема. При поступательном движении тела все его точки движутся по одинаковым (при наложении совпадающим) траекториям и имеют в каждый момент одинаковые (как по модулю, так и по направлению) скорости и ускорения.
Доказательство. Проведем из какой-либо точки, неподвижной относительно выбранной системы отсчета,
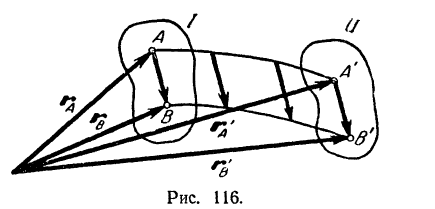
радиусы-векторы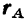 
и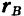 
двух каких-либо произвольных точек 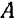и 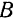тела (рис. 116). Из 
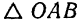следует, что
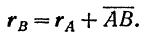
Так как тело движется поступательно, то при любом его перемещении вектор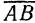 
, соединяющий точки 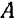и 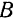тела и занимающий относительно тела неизменное положение, будет оставаться параллельным своему начальному положению и, следовательно, является постоянным вектором 
.
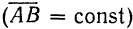Таким образом, при любом поступательном перемещении тела радиусы-векторы двух его произвольных точек, изменяясь, будут всегда отличаться друг от друга на один и тот же постоянный вектор. Так, при поступательном перемещении тела из положения I в положение II (рис. 116) будем иметь:
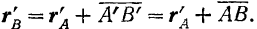
Следовательно, траекторию точки 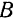можно получить, сместив траекторию точки 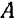в направлении вектора 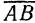на расстояние 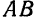, и потому эти траектории будут одинаковыми (совпадающими друг с другом при их параллельном переносе).
Продифференцировав по времени равенство (I), будем иметь:
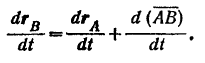
Но производная от постоянного вектора
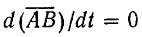
и поэтому
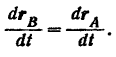
Производные же от радиусов-векторов точек 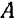и 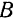дают, как известно (стр. 151), скорости этих точек
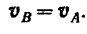
Дифференцируя вновь по времени последнее векторное равенство, будем иметь:
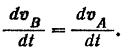
Производная же по времени от скорости точки дает ее ускорение (стр. 153) и, следовательно, мы получаем
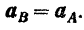
Мы доказали, что при поступательном движении тела две его произвольные точк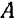и и 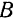движутся совершенно одинаково. Ясно, что этот вывод можно распространить и на все другие точки тела.
Из доказанной теоремы следует, что поступательное движение тела вполне определяется движением какой-либо одной его точки. Таким образом, задача изучения поступательного движения твердого тела сводится к уже рассмотренным ранее задачам кинематики точки.
Скорость и ускорение, общие для всех точек поступательно движущегося тела, называются скоростью и ускорением этого тела.
Заметим, что говорить о скорости и ускорении тела можно только в случае его поступательного движения. Во всех остальных случаях различные точки тела имеют различные скорости и различные ускорения.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
