Оглавление:
Как построить векторную диаграмму токов и напряжений
Расчеты в цепях с синусоидальными напряжениями и токами упрощаются, если вместо синусоид оперировать с их изображениями — вращающимися векторами (рис. 1).
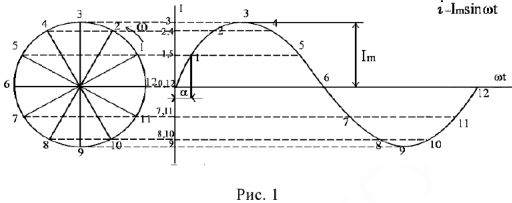
Проекция конца вектора на ось координат совершает синусоидальные колебания : каждое мгновенное значение тока, соответствующее моменту времени 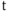 и фазовому углу
и фазовому углу 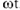 , можно рассматривать как проекцию на ось ординат вектора, повернувшегося на фазовый угол относительно оси абсцисс.
, можно рассматривать как проекцию на ось ординат вектора, повернувшегося на фазовый угол относительно оси абсцисс.
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Таким образом, синусоидальная функция условно представляется вектором, длина которого определяется максимальным или действующим ее значением, а направление — ее начальной фазой; положительная начальная фаза откладывается от горизонтальной оси в сторону вращения векторов (против часовой стрелки). Векторы токов и напряжений, вращаясь с одной и той же
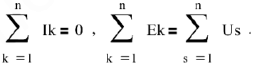
угловой скоростью 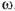 ,. неподвижны относительно друг друга. Условное изображение синусоидально изменяющихся во времени токов и напряжении при помощи векторов позволило записать в векторной форме первый и второй законы Кирхгофа.
,. неподвижны относительно друг друга. Условное изображение синусоидально изменяющихся во времени токов и напряжении при помощи векторов позволило записать в векторной форме первый и второй законы Кирхгофа.
Алгебраическому суммированию синусоид, т.е. суммированию их мгновенных значений, соответствуют геометрические действия над изображающими их векторами. Применение в этой форме законов Кирхгофа даст возможность путем построения векторных диаграмм достаточно просто и наглядно рассчитывать электрические цепи. Приступая к графическому расчету пеней переменного тока, следует помнить, что физические процессы на участках цепи с сопротивлением, индуктивностью, емкостью весьма различны.
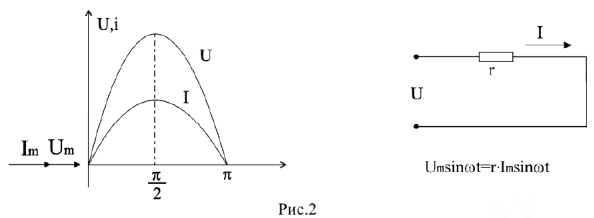
Соответственно вектор тока и вектор напряжения имеют одно направление.
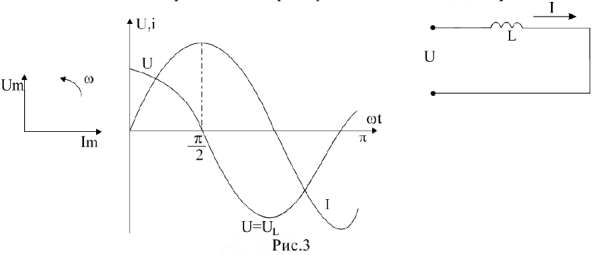
В индуктивном элементе ток отстает от напряжения на 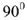 и соответственно располагаются векторы (рис.3). Закон Ома для участка цепи только с индуктивными сопротивлением записывается
и соответственно располагаются векторы (рис.3). Закон Ома для участка цепи только с индуктивными сопротивлением записывается 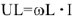 .
.
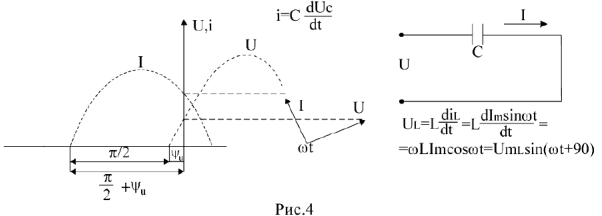
В емкостном элементе в активном сопротивлении ток и напряжение совпадают по фазе (рис.2), ток опережает напряжение на 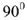 ( расположение вектора напряжения и тока показано на рис.4); закон Ома для участка цепи только с емкостным сопротивлением записывается
( расположение вектора напряжения и тока показано на рис.4); закон Ома для участка цепи только с емкостным сопротивлением записывается 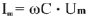 или
или 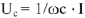 .
.
Рассмотрим расчет разветвленных электрических цепей с помощью векторных диаграмм.
Графоаналитический метод расчета
Графоаналитический метод расчета — это совокупность графического метода и метода пропорционального пересчета. Метод основан на том, что в линейной цепи токи пропорциональны напряжениям, векторная диаграмма напряжений и токов, рассчитанная и построенная для одного значения питающего цепь напряжения, сохранит свой вид при изменении величины этого напряжения, на диаграмме при этом изменятся лишь масштабы напряжений и токов.
Пример №1.
Для цепи (рис.5) известны параметры
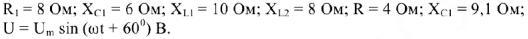
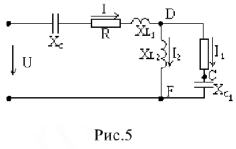
Требуется определить действующее значение токов ветвей, напряжений на участках цепи, начальные фазы токов и напряжений.
Построение векторной диаграммы начинается с наиболее удаленного источника элемента цепи, как говорят, с «конца» схемы. Принимаем масштабы для тока 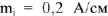 и для напряжения
и для напряжения 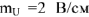 . Задаем значение тока в ветви
. Задаем значение тока в ветви 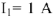 , определяем и строим на диаграмме напряжения на участках ветви
, определяем и строим на диаграмме напряжения на участках ветви 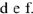 .
.
Падение напряжения на емкостном сопротивлении равно по величине 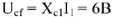 и отстает по фазе от тока
и отстает по фазе от тока 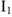 на 90° (вектор
на 90° (вектор 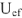 на диаграмме).
на диаграмме).
Падение напряжения на 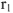 по величине равно
по величине равно 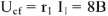 и совпадает по фазе с током
и совпадает по фазе с током 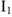 . Вектор напряжения ориентируем на диаграмме относительно тока
. Вектор напряжения ориентируем на диаграмме относительно тока 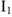 . Сумма векторов
. Сумма векторов 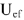 и
и 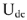 определяет напряжение на участке
определяет напряжение на участке 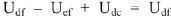 . Из диаграммы но масштабу
. Из диаграммы но масштабу 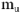 определяем величину напряжения
определяем величину напряжения 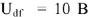 . Далее используем закон Ома для участка цепи с сопротивлением
. Далее используем закон Ома для участка цепи с сопротивлением 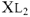 , находим ток
, находим ток 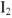 , так как
, так как 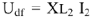 то
то 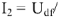
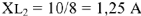 .
.
Для узла 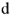 уравнение по первому закону Кирхгофа запишется
уравнение по первому закону Кирхгофа запишется 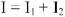 .
.
Определив величину тока 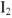 , построим вектор
, построим вектор 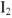 , приняв за начало построения коней вектора тока
, приняв за начало построения коней вектора тока 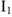 . Вектор тока
. Вектор тока 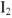 строится под углом
строится под углом 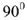 к вектору напряжения
к вектору напряжения 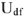 — в сторону отставания, так как ток
— в сторону отставания, так как ток 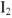 — ток через индуктивный элемент, он оттает от напряжения на
— ток через индуктивный элемент, он оттает от напряжения на 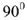 . Сумма векторов токов
. Сумма векторов токов 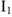 и
и 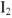 дает вектор
дает вектор  — ток в общей ветви цепи, он равен
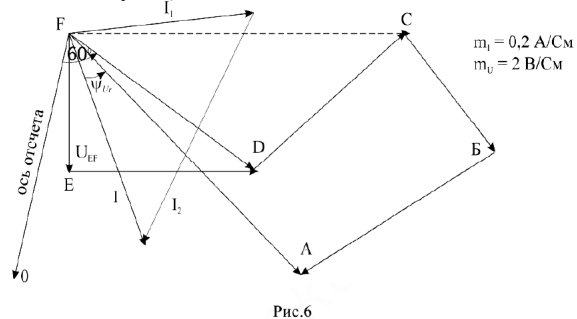
— ток в общей ветви цепи, он равен 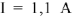 (взят в масштабе с диаграммы).
(взят в масштабе с диаграммы).
Запишем и графически решим уравнение по второму закону Кирхгофа для контура 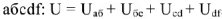 .
.
Перейдем к построению этого уравнения. Примем конец вектора 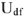 за начало построения вектора напряжения
за начало построения вектора напряжения 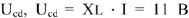 — падение напряжения на индуктивном сопротивлении. Вектор этого напряжения опережает по фазе ток
— падение напряжения на индуктивном сопротивлении. Вектор этого напряжения опережает по фазе ток  на
на 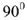 , строим его.
, строим его.
Принимаем конец вектора 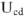 за начало построения вектора напряжения
за начало построения вектора напряжения 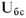 на активном сопротивлении. Величина напряжения
на активном сопротивлении. Величина напряжения 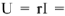
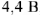 , вектор напряжения совпадает по фазе с током
, вектор напряжения совпадает по фазе с током  , строим его параллельно вектору тока
, строим его параллельно вектору тока  . Принимаем конец вектора
. Принимаем конец вектора 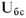 за начало построения вектора
за начало построения вектора 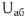 — напряжения на емкостном сопротивлении
— напряжения на емкостном сопротивлении 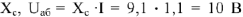 , вектор
, вектор 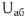 отстает на
отстает на 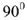 от вектора тока
от вектора тока  .
.
Если теперь соединим начало координат (точку  с концом вектора
с концом вектора 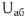 (точка «а» диаграммы напряжений), получим вектор приложенного к цепи напряжения
(точка «а» диаграммы напряжений), получим вектор приложенного к цепи напряжения 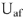 , равный 15В (с масштаба напряжений). Если напряжение, приложенное к цепи имеет другую величину, например, 90 В. то в силу линейности законов Кирхгофа все токи и падения напряжения увеличатся в
, равный 15В (с масштаба напряжений). Если напряжение, приложенное к цепи имеет другую величину, например, 90 В. то в силу линейности законов Кирхгофа все токи и падения напряжения увеличатся в 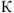 раз, где
раз, где 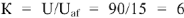 , но взаимное расположение вектором на диаграмме не изменится.
, но взаимное расположение вектором на диаграмме не изменится.
Входное напряжение имеет начальную фазу 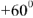 , учтем что и построим ось отсчета углов начальных фаз. К вектору напряжения
, учтем что и построим ось отсчета углов начальных фаз. К вектору напряжения 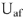 проведем луч
проведем луч 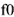 из начала построения (точка
из начала построения (точка  под углом
под углом 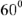 , луч
, луч 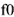 будет осью отсчета углов начальных фаз всех токов и напряжений.
будет осью отсчета углов начальных фаз всех токов и напряжений.
Пользуясь векторной диаграммой, можно записать мгновенные значения всех рассчитанных величин. Например, ток во второй ветви:
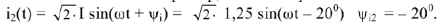
Напряжение участка 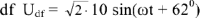 и т.д.
и т.д.
Построенная в такой последовательности векторная диаграмма напряжений носит название топографической.
Топографическая диаграмма
Топографические диаграммы представляют собой диаграммы комплексных потенциалов, причем каждой точке схемы соответствует определенная точка на топографической диаграмме.
Топографическая диаграмма позволяет измерить величину и начальную фазу напряжения любого участка цепи, не участвующею в расчете. Например,
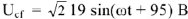
В действующее значение напряжения между точками 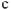 и
и  схемы
схемы 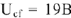 и начальная фаза
и начальная фаза 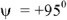 . тогда
. тогда
Рассмотрим пример построения топографической диаграммы на комплексной плоскости.
Пример №2.
Дана цепь (рис.7), её параметры:
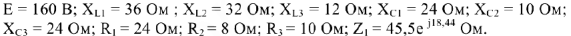
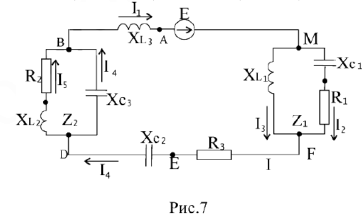
Комплексным методом рассчитаем токи цепи:
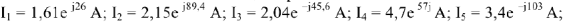
Строим на векторной плоскости диаграмму токов в масштабе 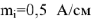 (рис.8). Для построения топографической диаграммы напряжений принимаем потенциал узла
(рис.8). Для построения топографической диаграммы напряжений принимаем потенциал узла 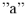 равным нулю,
равным нулю, 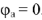 .
.
Тогда точка 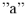 будет находиться в начале координат комплексной плоскости. Вычислим комплексы напряжении на каждом из элементов цепи, обходя из точки
будет находиться в начале координат комплексной плоскости. Вычислим комплексы напряжении на каждом из элементов цепи, обходя из точки 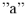 цепь против направления тока
цепь против направления тока 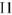 . При таком направлении обхода напряжение
. При таком направлении обхода напряжение 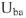 на сопротивлении
на сопротивлении 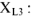
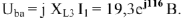
Строим вектор 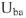 на комплексной плоскости (рис.8).
на комплексной плоскости (рис.8).
Из точки 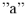 под углом
под углом 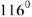 к действительной полуоси +1 откладываем модуль
к действительной полуоси +1 откладываем модуль 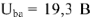 в масштабе
в масштабе 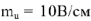 . Вершина построенного вектора соответствует точке
. Вершина построенного вектора соответствует точке 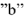 . Стрелку вектора
. Стрелку вектора 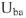 следует направить к точке
следует направить к точке 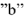 т.е противоположно направлению стрелки напряжения
т.е противоположно направлению стрелки напряжения 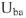 на схеме цепи, топографической диаграмме вектор
на схеме цепи, топографической диаграмме вектор 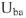 должен опережать но фазе вектор тока
должен опережать но фазе вектор тока 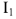 на 90°. Находим напряжение на сопротивлении
на 90°. Находим напряжение на сопротивлении 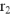 :
:
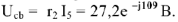
По полученному выражению из точки 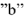 строим вектор
строим вектор 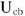 Вершиной вектора
Вершиной вектора 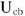 является точка
является точка 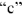 .
.
Контроль построения: вектор 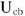 должен совпадать по фазе с вектором тока
должен совпадать по фазе с вектором тока 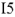 .Теперь находим напряжение на индуктивности
.Теперь находим напряжение на индуктивности 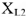 :
:
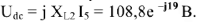
Из точки 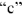 строим вектор
строим вектор 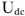 . Вершиной построенного вектора является точка
. Вершиной построенного вектора является точка 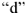 .
.
Контроль построения: вектор 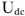 должен опережать по фазе вектор тока
должен опережать по фазе вектор тока 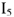 на
на 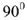 . Переходя по контуру в выбранном направлении, находим последовательно положение точек
. Переходя по контуру в выбранном направлении, находим последовательно положение точек 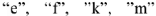 на комплексной плоскости. Вектор, соединяющий начало координат и точку
на комплексной плоскости. Вектор, соединяющий начало координат и точку 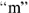 . представляет собой ЭДС источника
. представляет собой ЭДС источника 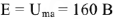 .
.
Пользуясь топографической диаграммой, легко определить напряжения между любыми точками цепи. Например, комплекс напряжения 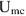 определяется вектором, соединяющим точки
определяется вектором, соединяющим точки 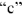 и
и 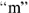 и направленным к точке
и направленным к точке 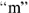 (показан на рис.8 пунктиром). Измеряя на диаграмме модуль и начальную фазу вектора
(показан на рис.8 пунктиром). Измеряя на диаграмме модуль и начальную фазу вектора 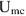 находим
находим 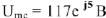 .
.
ПримсрЗ. Рассмотрим расчет цепи на рис.7 графоаналитическим методом
Зададимся условным значением тока 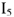 , пусть
, пусть 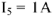 . В масштабе
. В масштабе 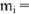
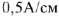 строим значение тока
строим значение тока 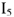 , полагая, что точка
, полагая, что точка 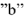 находится в начале координат. Выбранному условному значению тока
находится в начале координат. Выбранному условному значению тока 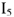 однозначно соответствуют условные значения всех остальных токов и напряжений в цепи. Эти напряжения и токи снабжаем меткой «штрих». Находим напряжение
однозначно соответствуют условные значения всех остальных токов и напряжений в цепи. Эти напряжения и токи снабжаем меткой «штрих». Находим напряжение 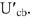
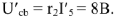
В масштабе 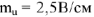 строим вектор напряжения
строим вектор напряжения 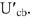 , совпадающий по фазе с вектором тока
, совпадающий по фазе с вектором тока 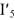 ( рис.9).
( рис.9).
Вычислив напряжение 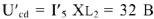 , строим вектор напряжения
, строим вектор напряжения 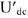 , опережающий по фазе вектор тока
, опережающий по фазе вектор тока 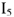 на 90′. Соединив точки
на 90′. Соединив точки 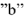 и
и 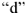 , получаем вектор
, получаем вектор 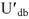 . Измеряя линейкой его длину с учетом масштаба напряжений, находим
. Измеряя линейкой его длину с учетом масштаба напряжений, находим 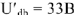 . По закону Ома находим ток
. По закону Ома находим ток 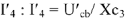
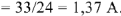
Из конца вектора тока 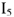 строим вектор тока
строим вектор тока 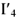 , опережающий по фазе вектор напряжения
, опережающий по фазе вектор напряжения 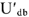 на
на 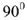 . Векторно суммируя токи
. Векторно суммируя токи 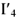 и
и 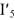 находим ток
находим ток 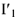 . Измеряя линейкой длину вектора тока
. Измеряя линейкой длину вектора тока 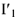 находим
находим 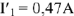 . Зная токи
. Зная токи 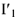 вычисляем напряжения
вычисляем напряжения 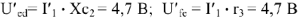 .
.
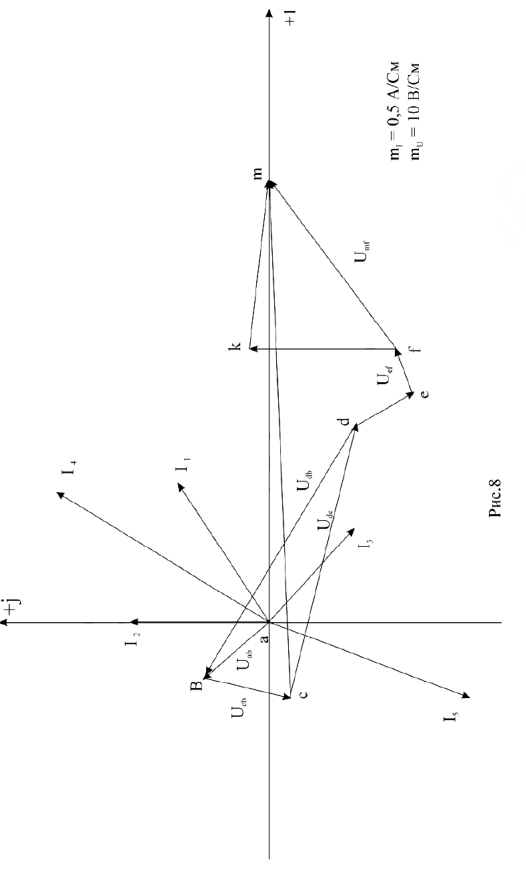
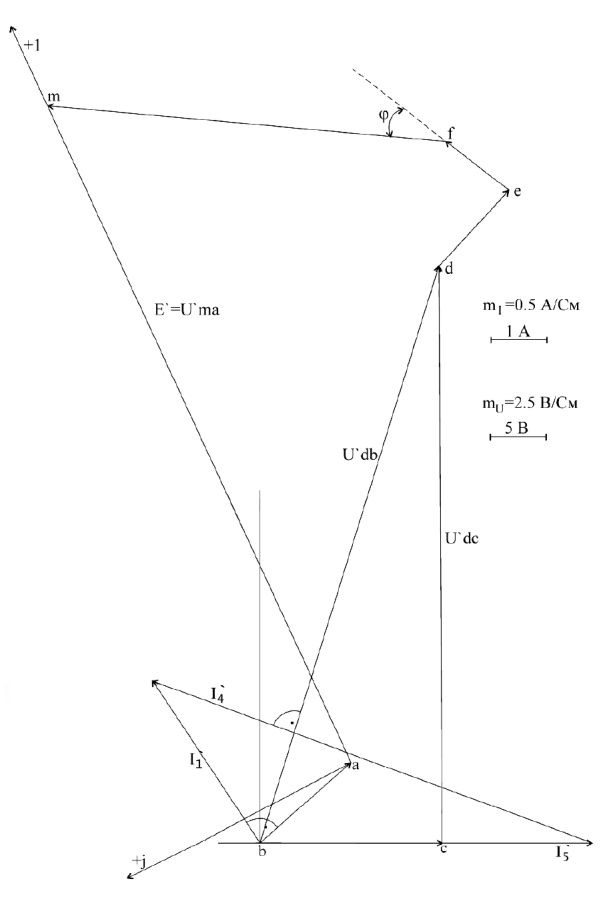
Рис.9
Из точки 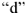 строим вектор напряжения
строим вектор напряжения 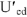 , отстающего но фазе от тока
, отстающего но фазе от тока 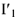 на
на 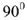 и вектор напряжения
и вектор напряжения 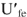 совпадающего по фазе с током
совпадающего по фазе с током 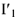 . Чтобы определить токи
. Чтобы определить токи 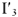 и
и 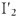 для участка
для участка 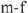 цепи, построим дополнительную векторную диаграмму
цепи, построим дополнительную векторную диаграмму 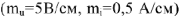 . Пусть
. Пусть
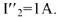
Тогда
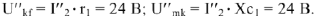
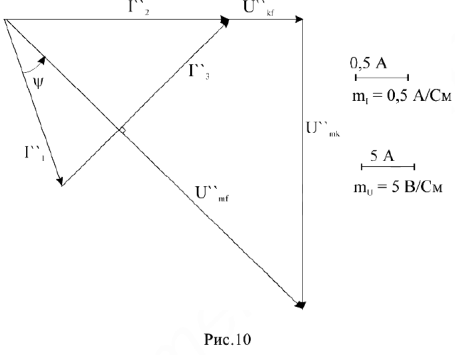
С учетом фазовых соотношений между током 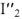 и напряжениями
и напряжениями 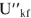 строим диаграмму (рис. 10). Измеряя длину вектора
строим диаграмму (рис. 10). Измеряя длину вектора 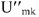 , с учетом масштаба напряжений находим его величину
, с учетом масштаба напряжений находим его величину 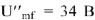 . Тогда величина тока
. Тогда величина тока 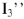 определяется следующим образом
определяется следующим образом 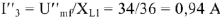 .
.
Построив вектор 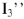 и суммируя векторы токов
и суммируя векторы токов 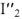 и
и 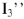 , из диаграммы на рис. 10 находим
, из диаграммы на рис. 10 находим 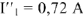 .
.
Чтобы привести диаграмму на рис.10 в соответствие с найденными ранее значениями тока 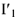 , находим коэффициент пересчета
, находим коэффициент пересчета
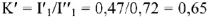
Умножая длины всех векторов на рис.10 на коэффициент 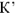 и сохраняя неизменными фазовые углы, получим векторную диаграмму участка
и сохраняя неизменными фазовые углы, получим векторную диаграмму участка 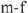 , соответствующую току
, соответствующую току 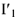 .
.
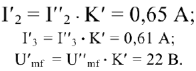
Измеряем угол 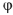 на диаграмме рис.10:
на диаграмме рис.10: 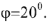
Под углом 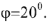 по отношению к вектору
по отношению к вектору 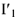 на рис.9 из точки
на рис.9 из точки 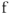 строим вектор
строим вектор 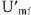 . Найдем теперь напряжение
. Найдем теперь напряжение 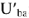 :
:
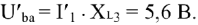
Поскольку напряжение 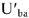 , опережает по фазе ток
, опережает по фазе ток 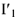 на 90°. то вектор
на 90°. то вектор 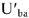 строится так, как показано на Рис.9. Соединяя точки
строится так, как показано на Рис.9. Соединяя точки 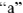 и
и 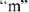 получаем вектор
получаем вектор 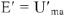 . Измеряя его длину находим
. Измеряя его длину находим
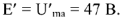
Векторная диаграмма на рис.9 является также и топографической диаграммой. ЭДС 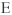 превышает ЭДС
превышает ЭДС 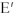 в
в 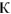 раз:
раз:
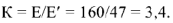
Поскольку рассчитываемая цепь линейна, то напряжения и токи, вызываемые ЭДС 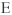 , превышают условные напряжения
, превышают условные напряжения 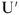 и токи
и токи 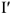 также в
также в 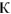 = 3.4 раза.
= 3.4 раза.
Таким образом

Чтобы измерить начальные фазы токов и напряжений, следует на рис.9 выбрать такую систему координат, в которой ЭДС 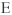 имеет соответствующую заданию начальную фазу. Так как
имеет соответствующую заданию начальную фазу. Так как 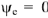 , то поместив начало координат в точку
, то поместив начало координат в точку 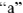 , действительную полуось совмещаем с направлением ЭДС
, действительную полуось совмещаем с направлением ЭДС 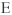 , а полуось
, а полуось 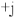 строим ортогонально оси 4 1, как показано на рис.9.
строим ортогонально оси 4 1, как показано на рис.9.
Рассмотрим пример построения векторной диаграммы по известным токам и напряжениям (действующие значения напряжений и токов получены экспериментально). В этом случае при помощи векторной диаграммы можно решить обратную задачу расчета цепи: но токам и напряжениям цепи определить эквивалентные параметры двухполюсников, составляющих цепь.
Пример №3.
Дана цепь (рис.11), известны показания измерительных приборов. Найдем параметры двухполюсника, эквивалентного данной схеме.
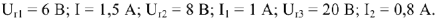
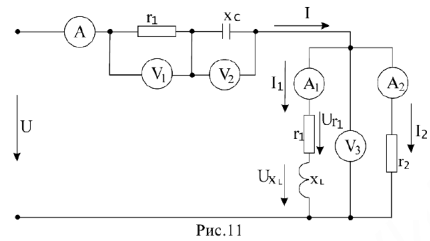
Для данной схемы можно составить три уравнения по законам Кирхгофа:
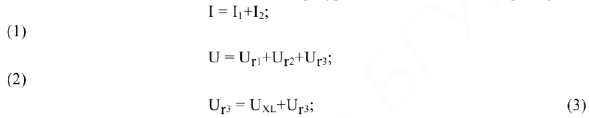
Решим эти уравнения графически. Построение диаграммы следует начать с построения вектора 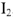 , для этой ветви известно взаимное расположение вектора тока и напряжения, участок с активным сопротивлением. В масштабе токов
, для этой ветви известно взаимное расположение вектора тока и напряжения, участок с активным сопротивлением. В масштабе токов 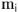 в произвольном направлении строится вектор
в произвольном направлении строится вектор 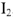 . Так как
. Так как 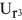 — падение напряжения па активном элементе, оно совпадает но направлению с вектором тока
— падение напряжения па активном элементе, оно совпадает но направлению с вектором тока 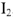 , в масштабе напряжений
, в масштабе напряжений 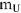 , строим этот вектор. Ток
, строим этот вектор. Ток 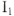 в ветви с индуктивной катушкой отстает от напряжений
в ветви с индуктивной катушкой отстает от напряжений 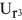 , на некоторый угол
, на некоторый угол 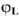 , который неизвестен.
, который неизвестен.
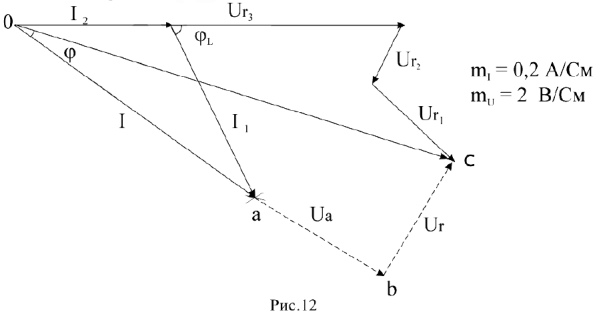
Используя показания амперметров 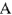 и
и 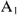 , решаем графически первый закон Кирхгофа (1) методом засечек: из конца вектора тока
, решаем графически первый закон Кирхгофа (1) методом засечек: из конца вектора тока 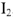 делаем засечку радиусом, равным величине тока
делаем засечку радиусом, равным величине тока 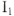 в сторону отставания от напряжения
в сторону отставания от напряжения 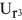 , а из начала построения т.О вектора
, а из начала построения т.О вектора 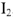 делаем засечку радиусом, равным току
делаем засечку радиусом, равным току 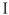 . Получаем векторную диаграмму токов заданной схемы. Из построения теперь можно определить
. Получаем векторную диаграмму токов заданной схемы. Из построения теперь можно определить 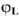 — угол сдвига по фазе между током и напряжением на катушке.
— угол сдвига по фазе между током и напряжением на катушке.
Далее достраивается диаграмма напряжений: напряжения 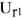 и
и 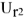 известны. падение напряжения на емкости отстает от вектора тока ветви
известны. падение напряжения на емкости отстает от вектора тока ветви 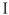 на 90°, строим его из конца вектора
на 90°, строим его из конца вектора 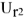 ,
,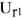 — падение напряжения на активном элементе совпадает с током ветви, строим из конца
— падение напряжения на активном элементе совпадает с током ветви, строим из конца 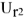 в направлении, параллельном току
в направлении, параллельном току 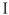 .
.
Замыкающий вектор на диаграмме напряжений соединяет начало построения и конец вектора 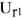 , определяет в масштабе напряжение
, определяет в масштабе напряжение 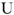 на входе схемы, он равен
на входе схемы, он равен 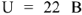 .
.
Теперь с помощью треугольников напряжений (сопротивлений), токов (проводимостсй), построенных для какого-либо участка цепи или для всей цепи можно найти сопротивления, проводимости и параметры двухполюсника.
Определим эквивалентные параметры всей цени заданной схемы (см. рис.11) 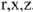 . Сначала строится треугольник напряжений
. Сначала строится треугольник напряжений 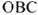 : из конца вектора
: из конца вектора 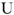 опускается перпендикуляр па направление вектора тока
опускается перпендикуляр па направление вектора тока 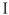 и определяется активная и реактивная составляющие напряжения —
и определяется активная и реактивная составляющие напряжения — 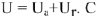 . С учетом масштаба
. С учетом масштаба 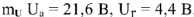 .
.
- По закону Ома можно подсчитать эквивалентное активное сопротивление схемы
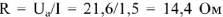 эквивалентное реактивное сопротивление
эквивалентное реактивное сопротивление 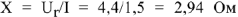 и модуль полного сопротивления схемы
и модуль полного сопротивления схемы 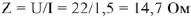 .
.
Векторная диаграмма сложной электрической цепи
Векторная диаграмма для сложной электрической цепи может быть построена только после расчета этой цепи; строится она на комплексной плоскости по известным комплексам токов всех ветвей и комплексам напряжений на каждом элементе цепи. Пример 5. Заданы источники энергии, сопротивления схемы 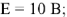
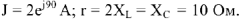
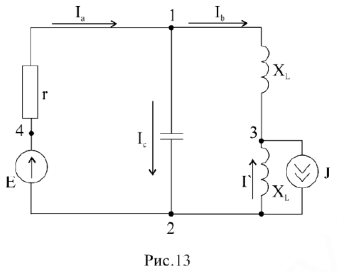
В результате расчета определены токи в ветвях:
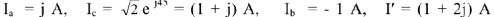
и падения напряжений на каждом элементе схемы:
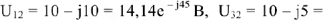
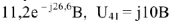
Для построения векторной диаграммы составим уравнение по первому и второму законам Кирхгофа в общем виде и в численном выражении:
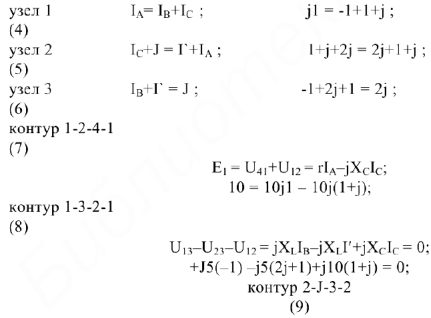
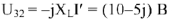 — напряжение на участке с источником тока.
— напряжение на участке с источником тока.
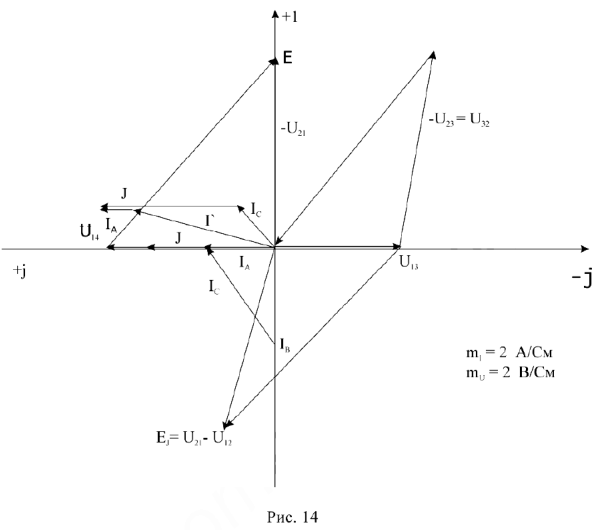
Приступим к построению уравнения (4). В выбранном масштабе токов 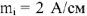 на комплексной плоскости (Рис.14) строим ток
на комплексной плоскости (Рис.14) строим ток 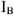 , из его конца — ток
, из его конца — ток 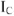 . Соединяем начало координат с концом вектора тока
. Соединяем начало координат с концом вектора тока 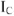 , получим вектор тока
, получим вектор тока 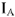 (построение можно вести по модулю комплекса тока и аргументу, можно строить действительные и мнимые составляющие токов).
(построение можно вести по модулю комплекса тока и аргументу, можно строить действительные и мнимые составляющие токов).
Построена векторная диаграмма токов, отображающая уравнение (4). Для узла 2 графически решаем уравнение (5); из начала координат строим комплекс тока 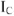 , к току
, к току 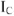 прибавляя ток источника тока J, сумма этих токов по уравнению (5) равна сумме комплексов токов
прибавляя ток источника тока J, сумма этих токов по уравнению (5) равна сумме комплексов токов 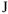 и
и 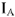 , из начала координат строим ток
, из начала координат строим ток 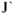 , из его конца — ток
, из его конца — ток 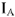 . Получаем замкнутый многоугольник. Гак как по 1 закону Кирхгофа независимых уравнений может быть составлено два, ограничиваемся построенными на диаграмме двумя уравнениями.
. Получаем замкнутый многоугольник. Гак как по 1 закону Кирхгофа независимых уравнений может быть составлено два, ограничиваемся построенными на диаграмме двумя уравнениями.
- Перейдем к построению двух независимых уравнений второго закона Кирхгофа (7 и 8).
Из начала координат строим комплекс напряжения 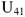 — напряжение на участке с активным сопротивлением совпадает по направлению с током
— напряжение на участке с активным сопротивлением совпадает по направлению с током 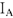 . Из конца
. Из конца 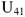 строим
строим 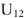 — напряжение на емкости (это паление напряжения отстает от тока
— напряжение на емкости (это паление напряжения отстает от тока 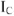 на 90°), сумма этих комплексов напряжений равна комплексу ЭДС
на 90°), сумма этих комплексов напряжений равна комплексу ЭДС 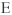 , действующей в цепи — соединяем начало построения т. О с концом комплекса напряжения
, действующей в цепи — соединяем начало построения т. О с концом комплекса напряжения 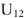 .
.
Комплекс ЭДС 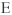 был задан действительным числом , так мы и получили на диаграмме: вектор напряжения
был задан действительным числом , так мы и получили на диаграмме: вектор напряжения 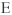 направлен по действительной оси.
направлен по действительной оси.
Для контура 1-3-2-1 строится комплекс напряжения 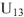 . Вектор
. Вектор 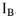 из конца
из конца 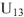 строим напряжение —
строим напряжение —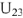 , замыкающим вектором будет напряжение —
, замыкающим вектором будет напряжение —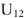 (алгебраическая сумма комплексов напряжений в этом контуре равна 0). Используя векторную диаграмму, моно графически определить напряжение источника тока
(алгебраическая сумма комплексов напряжений в этом контуре равна 0). Используя векторную диаграмму, моно графически определить напряжение источника тока 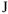 , обозначим его
, обозначим его 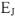 . Для контура 1-3-
. Для контура 1-3-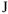 -2-1 уравнение но второму закону Кирхгофа
-2-1 уравнение но второму закону Кирхгофа 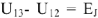 . На диаграмме вычтем из комплекса
. На диаграмме вычтем из комплекса 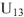 напряжение
напряжение 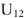 , получим .
, получим .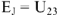 .
.
Возможно эти дополнительные страницы вам будут полезны:

