Оглавление:




Построение разверток пирамидальных, конических и других линейчатых поверхностей, исключая цилиндрические
- Строительные разработки для пирамидальных, конических и других линейных поверхностей, кроме цилиндров 1. Конструкция развития этих поверхностей вырезана (или описана) в естественный вид треугольников, составляющих заданную поверхность конуса, или заданной конической или линейчатой поверхности, на которую эта поверхность заменяется Это приводит к повторному построению многогранной поверхности.
- Этот метод называется методом треугольника (триангуляция), потому что он разбивает поверхность на треугольники. 2. Если вы игнорируете графические ошибки, построенная развертка такой поверхности может считаться точной. Пример. Создайте полное сканирование части треугольной пирамиды SABC, окруженной базовой плоскостью и второй фронтальной плоскостью проекции 2 (рис. 212).
Показывает применение этого метода к поверхности пирамиды. Людмила Фирмаль
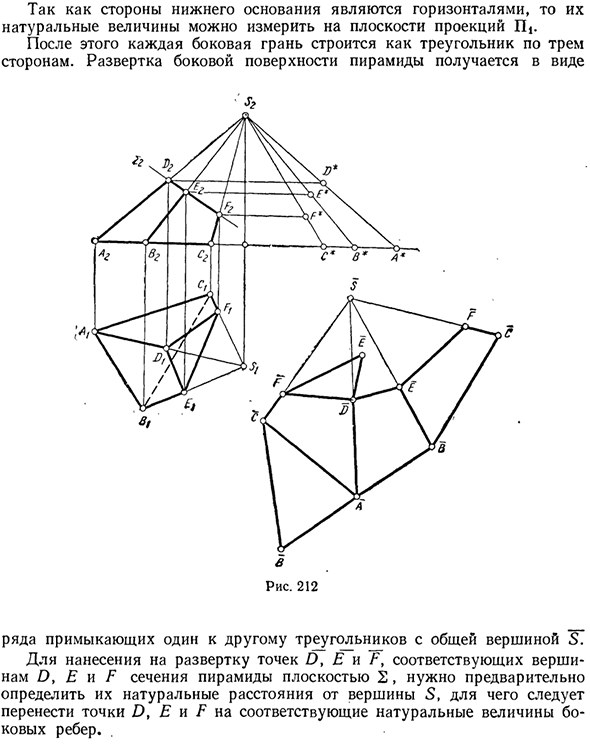
Во-первых, вам нужно построить боковое сканирование всей пирамиды SABC. Поскольку стороны пирамид представляют собой треугольники, для построения их развития необходимо построить естественные типы этих треугольников. Для этого сначала необходимо определить естественную ценность боковых ребер. Боковые ребра можно определить с помощью прямоугольных треугольников.
Каждый треугольник представляет собой точку S, в которой одна нога превышает точки A, B, C, а вторая нога представляет собой отрезок, равный горизонтальной проекции соответствующего бокового ребра. 1 Эта особенность развертываемых линейчатых поверхностей устанавливается в процессе дифференциальной геометрии. Поскольку нижняя сторона горизонтальна, их естественные значения могут быть измерены в плоскости проекции IIj.
Каждая сторона тогда настроена как трехсторонний треугольник. Развитие стороны пирамиды получается в следующем виде Рисунок 212 Ряд смежных треугольников с общей вершиной 2G. Чтобы нарисовать точки D, E и F, соответствующие вершинам D, E и F сечения пирамиды с плоскостью 2 на скане, сначала необходимо определить естественное расстояние от вершины D Естественные значения E и F, чтобы сделать.
После создания бокового сканирования усеченной пирамиды добавьте треугольники ABC и DEF. Это естественный тип усеченного основания пирамиды. 3. Подумайте о создании конической развертки. Несмотря на то, что конические поверхности являются расширяемыми и, следовательно, имеют теоретически точные развертки, эти приблизительные развертки фактически строятся с использованием треугольного метода.
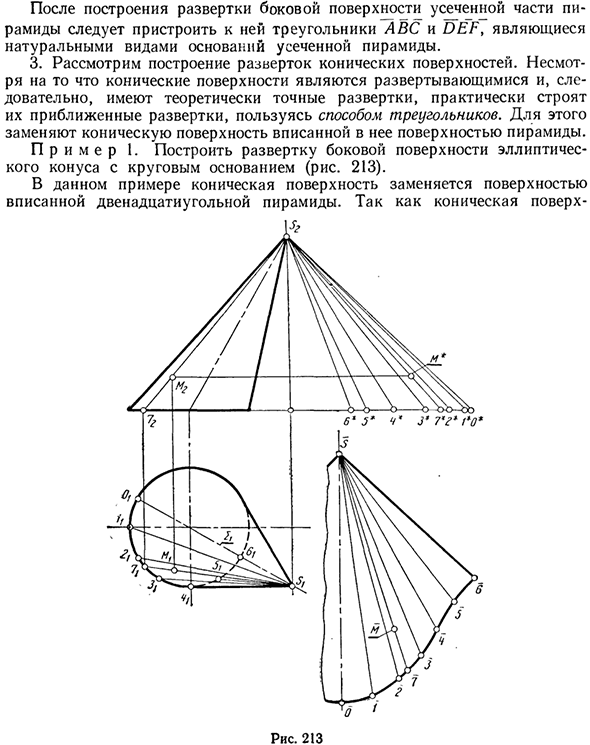
Для этого замените коническое лицо на вырезанное на нем лицо пирамиды. Пример 1. Создайте боковое сканирование эллиптического конуса с круглым дном (Рисунок 213). В этом примере поверхность 12-пирамиды, которая вписана конической поверхностью, заменяется. Потому что это коническая поверхность Поскольку структура имеет плоскость симметрии 2, вы можете построить сканирование только половины поверхности.
Разделите на 6 равных частей от половины точки O окружности основания конической поверхности, определите естественное значение генератора, нарисованного в точке разделения, используя прямоугольный треугольник, и 6 соседей с общей вершиной S Чтобы построить треугольники. Каждый из этих треугольников построен с трех сторон.
- В этом случае две стороны равны естественному значению генератора, а третья сторона является хордой, которая затягивает дугу основного круга между соседними точками разделения. Затем через точки O, 1, 2, … на дне конической поверхности, изогнутой хордовым методом, рисуется гладкая кривая.
С его помощью определяют натуральный размер генератора С-7, который проходит через точку М. Из них нарисуйте прямую линию S-7 на развороте, определите точку 7 по равному состоянию аккордов 2, -7, = 2-7 и поместите на нее расстояние SM- • S2M *.
Если вам нужно нарисовать точку M на поверхности сканирующего конуса, сначала вам нужно построить точку M * на гипотенузе S2-7 * прямоугольного треугольника. Людмила Фирмаль
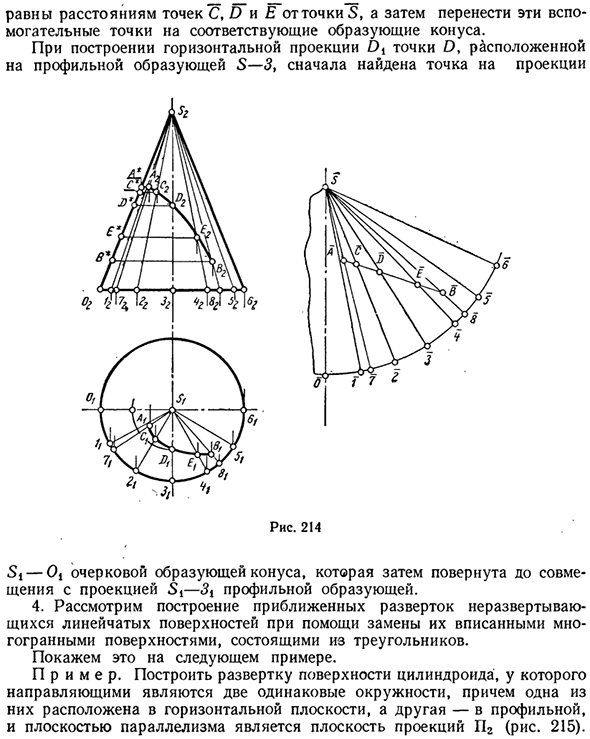
Пример 2. Нарисуйте геодезическую линию между точками A и B на поверхности заданного вращающегося конуса (Рисунок 214). Чтобы нарисовать нужную геодезическую линию, сначала нужно создать боковое сканирование конуса. Это сканирование представляет собой круговой сектор с радиусом, равным естественной величине шины конуса, и длиной дуги, равной окружности основания конуса.
На практике секторная дуга определяется с помощью этой строки. Эта строка считается равной строке, которая сокращает дугу основания конуса. Другими словами, поверхность конуса заменяется поверхностью вписанной пирамиды. Поскольку точки A и B находятся в передней половине поверхности конуса, на рис. 214 построено сканирование только этой половины поверхности.
Используя генераторы 5-7 и S-8, точки A и B существовали и нашли соответствующие точки A и B на скане. В то же время предварительный эскиз параметра 52-02 Естественное значение генератора конуса определяет натуральные величины S2A * и S2B * расстояния между точками A и B от вершины конуса 5_.
Соедините точки развертки A и B прямыми сегментами и отметьте точки C, O и I на пересечениях на линиях S-2, S-3 и S-4, соответствующих генераторам S-2, S-3 и S- вы. Рисунок 4 Равно расстоянию между точками S, C, D и E точки S, перенесите эти вспомогательные точки в соответствующий генератор конуса.
При создании горизонтальной проекции точки D в генераторе профилей S_3, точка на проекции определяется первой S, -Oj контурным генератором конуса. Затем он вращается, чтобы соответствовать проекции St-St шины профиля. 4. Рассмотрим построение приблизительного скана линейчатой поверхности, которую нельзя развернуть, заменив ее вписанной многогранной поверхностью, состоящей из треугольников. Это показано в следующем примере.
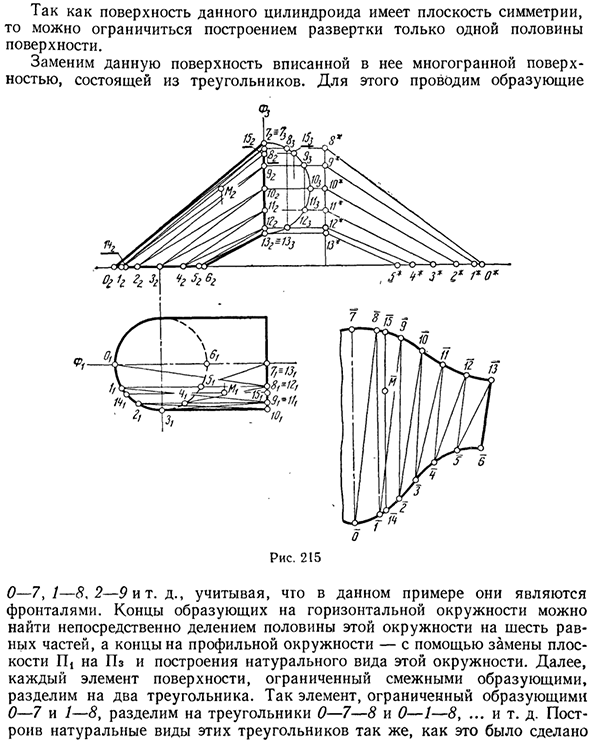
Пример. Создайте скан поверхности цилиндра. Направляющие представляют собой два одинаковых круга, один в горизонтальной плоскости, другой в профиле, а параллельная плоскость является плоскостью проекции G12 (рис. 215). Поскольку поверхность этого цилиндра имеет плоскость симметрии, вы можете ограничить ее построением сканирования только половины поверхности.
Замените эту поверхность вписанной многогранной поверхностью, состоящей из треугольников. Для этого запустите генератор Рис. 215 0-7.1-8.2 — Лит. д. В этом примере предположим, что это фронт. Конец генератора на горизонтальном круге можно найти непосредственно, разделив половину этого круга на шесть равных частей.
Край профиля окружности заменяет плоскость IIj на P3, чтобы создать естественный вид этого круга. Кроме того, каждый элемент поверхности, окруженный соседними генераторами, разделен на два треугольника. Поэтому элементы, окруженные генераторами 0-7 и 1-8, делятся на треугольники 0-7-8, 0-1-8, … и т. Д. Постройте так же, как вы создали естественную форму этих треугольников.
В примере 1 (см. Рис. 213) прохождение гладкой кривой к вершине дает приблизительное сканирование цилиндрической поверхности. Чтобы нарисовать произвольную точку М на скане на поверхности цилиндра, нарисуйте прямую линию 14-15 на скане, соответствующую шине 14-15, где расположена точка М, и расстоянию 15-М на ней. = 15 г-М2 должен быть поставлен.
Смотрите также:
Начертательная геометрия 1 курс

