Оглавление:




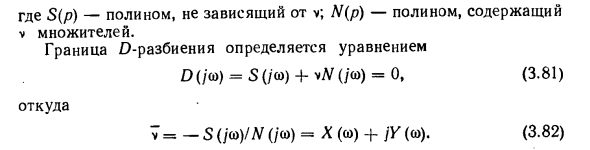



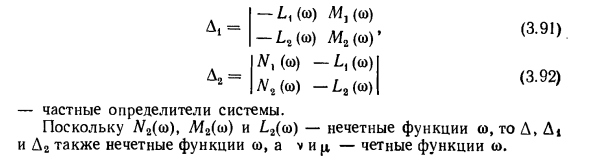










Построение областей устойчивости в плоскости параметров системы
- Построение устойчивых областей в плоскости параметров системы В очень важном исследовании устойчивости изучалось построение области устойчивости в плоскости одного или любых двух параметров, ее влияние на устойчивость и для различных фиксированных значений третьего параметра. В плоскости двух параметров строится семейство устойчивых областей. Граничное уравнение области устойчивости можно найти с помощью любого критерия устойчивости. Однако на практике почти всегда используется наиболее распространенный метод построения стабильных регионов — Ю.А. Предложил И. Неймарк и назвал метод разбиения D.
Буду разлагать концепцию. Рассмотрим характеристическое уравнение замкнутой системы порядка n. Это всегда делается путем деления на множитель с переменной высшего порядка p. D (p) = pn + fliP «» 1 + ••• + an = 0, (a0 = 1). (3,76) Представьте себе n-мерное пространство, координатными осями которого являются коэффициенты уравнения (3.76). Это пространство называется коэффициентом пространства. Каждая точка в пространстве коэффициентов соответствует определенному количеству коэффициентов в уравнении (3.76) и соответствующему многочлену степени l.
Уравнение (3.76) имеет n корней, и положение корня p на комплексной плоскости зависит от значения коэффициента при. Людмила Фирмаль
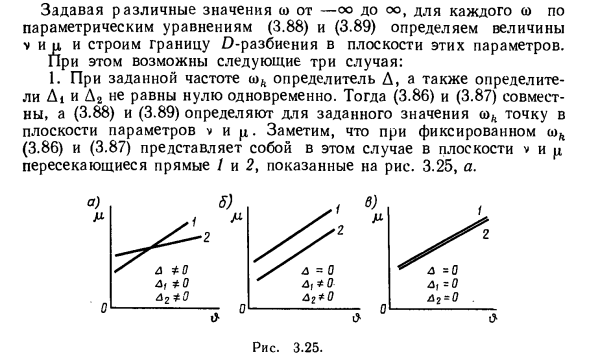
Построить O границ раздела в плоскости этих параметров. В этом случае есть три возможных случая: Далее (3.86) и (3.87) совместимы, а (3.88) и (3.89) определяют точку на плоскости параметра v для заданного значения o) Λ. В этом случае фиксированные плоскости vk (3.86) и (3.87) v и µ 3.25, пересекающие прямую линию / и 2, как показано на фиг. Рисунок 3.25. l 、 -Оy2-О дг * 0 о о о 2. При некоторых значениях u> k определитель D исчезает, а определители D4 и D2 не равны нулю. В этом случае (3.86) и (3.87) не совместимы и не имеют конечного решения. Как показано на рисунке 1, линии / и 2 параллельны и не пересекаются. 3.25, б. 3.
Для некоторых случаев определитель D и оба определителя D4 и D2 одновременно равны нулю. После этого v и q становятся неопределенными. В этом случае, как известно, одно из уравнений (3.86) и (3.87) приводит к другому и отличается определенным коэффициентом. Линии / и 2 (рис. 3.25, в) сливаются друг с другом, поэтому в плоскостях v и jj данной поверхности уравнение не является точкой + (Q Af, ((ofc) + Lt (o),) = 0 Поскольку все точки этой линии имеют одинаковое значение частоты ω = (Oy, вы не можете установить направление движения вдоль линии при изменении ω), поэтому специальная линия не применяется к кривой разложения D нет. Для большинства практических задач получена особая линия для значения а) = 0u = oo.
- В этом случае, по меньшей мере, один из коэффициентов v включается в коэффициент, соответствующий свободному a0 и наибольшему ap членам характеристического уравнения. Сингулярная линия с ω = 0 получается путем задания коэффициента равным нулю, а особая линия с ω = oo получается путем задания коэффициента v0 равным нулю. Если and и an не зависят от v и µ, этих специальных линий не существует. После того, как граница между D-разложением и особой линией построена, она должна быть закрашена с использованием следующего правила: при увеличении от -∞ до oo граница D-разложения находится на левой стороне, если D> 0, D < Если это 0, то оно заштриховано справа. Как и выше, vhu является четной функцией от ω, поэтому граница разложения D совпадает с положительными и отрицательными значениями частоты.
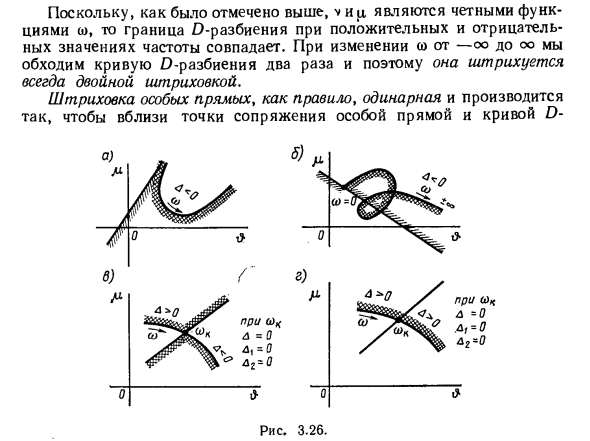
При переходе от -oo к oo кривая разложения D обходится дважды, поэтому она всегда выводится с двойной штриховкой. Штриховка сингулярной линии обычно одиночная и выполняется вблизи точки сопряжения сингулярной линии и кривой D-. Рисунок 3.26. Перегородки, разделяющие затененные и незатененные стороны линии и кривой, были ориентированы друг к другу (рис. 3.26, а и б).
В относительно редком случае, когда особая линия встречается с конечным значением частоты ω = o> h = £ 0, если A проходит через ноль и меняет знак, то особая линия заштрихована в соответствии с вышеуказанными правилами. Людмила Фирмаль
Однако он заштрихован дважды (рис. 3.26, в). Если при ω = coft ^ = 0 возникает особая прямая линия, и в то же время знак не меняется при прохождении A через ноль, специальная прямая линия не заштриховывается и исключается из рассмотрения (рис. 3.26, d). Отметим, что знак определителя A, определенный в (3.90), зависит от порядка членов в (3.86) и (3.87). Чтобы избежать существенных ошибок при применении штриховки, в (3.86) и (3.87) сначала опишите параметр, который откладывается вдоль горизонтальной оси, то есть термин, который включает в себя v, а затем откладывает на оси y. Вы должны написать термин, который включает в себя указанный параметр. с.
После применения штриховки определяется стабильная область, то есть область, которая претендует на то, чтобы быть областью, куда направляется штриховка. Затем выберите значения v = v0, η = | 00 »в этой области, подставьте их в характеристическое уравнение и используйте критерии устойчивости, рассмотренные выше, чтобы определить, являются ли все корни характеристического уравнения левосторонними. Вы должны решить, используя один. В этом случае, если не все корни не оставлены, в плоскости параметров v и q нет устойчивой области.
Другими словами, изменение только v и y не может стабилизировать систему. Однако, если найдены все корни, рассматриваемая область фактически является областью устойчивости D (0). После этого область D (m) может быть отмечена в любой другой точке на плоскости параметров v и µ. Пересечение границы раздела D (или особой линии с двойной штриховкой) из заштрихованной зоны в зону без тени, левую полуплоскость W * ‘, корень вправо, и наоборот. {w Пересечение особой линии и одного штриховки соответствует одному маршруту перехода. Пример 3.7 Характеристическое уравнение для замкнутой системы автоматического управления D (p) = (1 + Txp) (1 + 7 «(I + T9p) + K = 0,
Где К — усиление открытой системы. T1, Tg и T3 — постоянные времени для каждого динамического канала. Граница D-разбиения должна быть построена в плоскости усиления системы разомкнутого контура K. Опишите характеристическое уравнение в формате D (p) = S (p) -f- ~ N (p) = 0. Где S (p) = (l + 7>) (l + 7>) (l + 7>); N (p) = I; / <о, получить выражение Подставляя границу разложения D в характеристическое уравнение p: D (/ w) = (1 + / Г3) + К-S (/ о) + viV (/ о>) = О, Откуда ~ = K = -S (i «) / N (/ co) = — (1 + /» G «) (I-f / coG2) (I + / coG3) = X (co) + / G и 4 J Y ((i>) * Jm t> ^ 2G a> »0 K D (1) Рисунок 3.27. * ((*) = Re O- В * H = (TxTt + TgTb + TtT3) α-1; k (co) = co (7 \ Ga7 >> * — (T \ + T, + T)]. Учитывая различные значения частоты (o> 0), определите X ( 0 (пунктирная линия на рисунке 3.27). Затем, когда частота меняется с -oo на oo, проведите левую кривую D-сегмента вдоль обхода.
Кривая разбиения D делит плоскость на три области — /, // и ///. Кандидатом в стабильный регион является регион /, потому что люк направлен на него. Чтобы проверить, является ли эта область действительно стабильной, установите значение nТ0 == 0 в этой области, подставьте его в характеристическое уравнение, и полученное характеристическое уравнение b (p) = (1 4- 7ip) (l-J-T2p) x X (1-ТT3p) = 0, потому что все ядра pi = => — 1/7 \, pa = -1 / Tg и p9 = -1 / T3 остаются Область I — стабильная область D (0).
Поскольку коэффициент усиления K не является сложным, нас интересует только стабильный сегмент AB, который совпадает с действительной осью в стабильной области. Является ли значение K -I << K / o в характеристическое уравнение дает уравнение для границы D-разложения. O (/ a)) = 5 (/ o) (/ o,) = (1-I- / > (1 + / 0) ^ (1+ / a> rz) = 0, Откуда 7 = Г, = -1 (1 + / сГ2) (1 4- / VT3) + / (1 / [/ ш (1 + / 0,7-2) (I + / о, Г8)] + / K (сустав). Рисунок 3.28. Для различных значений частоты ω можно рассчитать X (<о) и К (<о), чтобы построить границу раздела D. Это показано на рисунке. 3,28.
Эта кривая вылупляется влево вдоль байпаса, когда частота w меняется с -oo на ooo. Кривая делит плоскость на четыре области (/, II, III, IV). Претендентами на стабильные районы являются Район / и III. Проверьте, является ли регион / действительно стабильным регионом. Когда T \ = 0, характеристическое уравнение D (p) <= * (Tpr-> I) (Tpr + 1) + + K = 0 является квадратным уравнением с положительным коэффициентом, поэтому все левые корни У меня есть это. Строго говоря, область / соответствует 74Φ0, а характеристическое уравнение имеет третью степень. При уменьшении γ один из корней характеристического уравнения перемещается влево в плоскости корня и становится отрицательной бесконечностью при Ti => = 0.
Исходя из теоремы о том, что корень непрерывно зависит от коэффициентов уравнения, можно утверждать, что система остается стабильной не только в 74-0, но и в некоторых областях с небольшими значениями 7 . Следовательно, площадь / является областью устойчивости D (0). То же самое можно показать, найдя корень характеристики Подставляя значение 74 в область I Затем пересечь кривую D-разбиения относительно количества и направления штриховки и отметить области D (I) и 0 (2). Отметим, что в этом случае существуют две устойчивые области O (O). Поскольку 74 — действительное число, меня интересует стабильный сегмент, соответствующий части горизонтальной оси в стабильной области. Система стабильна при 0 <74 <7 ^ и 74> 7 ^.
Система становится нестабильной при 7 ^ s + (T2 + T3) + p \ + ft + r27V 4- (T2 + T) p + 1 = Где v = 74, [х-к. Подстановка р = / оо в характеристическое уравнение дает уравнение для границы разложения D. D (/ «) = v / V (/») + | tM (/ «,) + L (/») = 0, N (/ «) — [Г2Г„ (/ «) • -f (Т2 + Г3) (/») + / «]; / ((/ O,) = 1, L (/)) = Г2Г3 (/ -) ++ + (A + 7 *,) 0m) + * • = (Г2Гз «r-1) o>. Если действительная и мнимая части равны нулю, получается следующая система уравнений: , ~ V (ΓΓΓ8) o> 3 + f (1-Γ27> ff = = 0, -v <Γa> 8-a>) + 0 • | v = (Γ, + Γ8) / (7 \ D> »-I); μ = Г27> З_ 1 + (Г2 + TS) W / (T2T3 <** — I). Основные детерминанты системы I- (T2 + G3) «» I D = …
При изменении коэффициента в уравнении (3.76), вследствие непрерывной зависимости от коэффициента, его корень перемещается в комплексной плоскости корня, описывая корневой годограф. Чтобы представить вышесказанное геометрически, рассмотрим кубическое характеристическое уравнение (n-3) (3,77) D (P) = P3 + 1P2 + agP + = 0 Взятие трех осей, перпендикулярных друг другу, и построение графиков значений их коэффициентов aia2 и a3 дает трехмерное пространство для коэффициентов. Каждая точка соответствует отдельному многочлену третьего порядка и трем различным корням комплексной корневой плоскости p (рис. 3.22). 5) ° 2 а) / Я В ♦ s
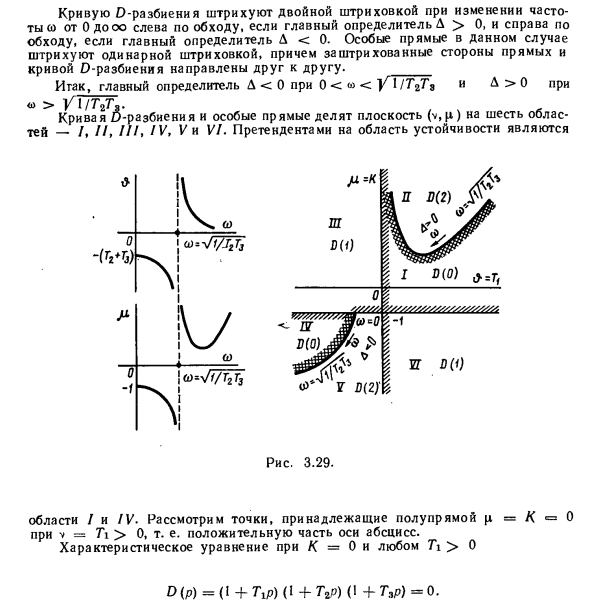
Чехия ФОМ 0 П, М + Рабочая группа N Z в * и Sz 7 П, 6 Рисунок 3.22. Например, точка М с координатами ах, ом, а3m является полиномом Dm (p) = p3 + a \ mp% + a? Соответствует Mp + Ozl и имеет три маршрута P \ m, P2M, pm в плоскости маршрута (рис. 3.22, а) N с различными точками, например, координатами и Лздздг, полином dn (p) = p34 Соответствует -a \ Np2 + a2Np + a, а его корнями являются p] Nt p2N и p3N. Для некоторых значений коэффициентов в уравнении (3.77) один из корней входит в начало координат, или пара корней находится на мнимой оси. То есть корень имеет вид 0 или ± / coL, поэтому соответствующая точка в пространстве параметров удовлетворяет уравнению (3,78) R (/ C) = OCH) 3 + a, (/ co) 2 + a2 (/ co) 4- = 0 Кривая D-разбиения заштрихована с двойной штриховкой, когда частота изменяется от 0 до oo в левом байпасе, когда основным определителем является D> 0, и заштрихована с правым байпасом, когда основным определителем является D <0 , и Кривые перегородки D обращены друг к другу. _ И взломать, основной определитель D <0
VI / Г2Го D> 0 в случае 0. Кривые D-разбиения и особые линии делят плоскость (v, µ) на шесть областей — /, //, III, IV, V и VI. Заявители по устойчивому развитию 0 м л (oWf / JM w 0) 0 -1 L 0, т.е. положительную часть горизонтальной оси. Характеристическое уравнение для K = 0 и T1> 0 D (p) = (I + Подсказка) (I + Tn) (I + 7 »= 0. В результате все три корня характеристического уравнения в этом случае остаются pi = »- 1/7 * 1, pg => -UT2 и p3 = -I / T3. Следовательно, поскольку положительная часть горизонтальной оси принадлежит стабильной области O (O), вся область также является стабильной областью.
Пройдите из этой области в другие области через D-раздел или границу единственной линии и отметьте оставшиеся области D (I) и D (2). Отметим, что в этом случае существуют две устойчивые области D (0). Однако мы сосредоточимся только на стабильной области D (0), которая соответствует физически возможному положительному значению с постоянной времени Γ1> 0. Построение границы раздела D в плоскости двух параметров дает общую картину влияния этих параметров на устойчивость системы. Если значение усиления K мало, система стабилизируется при любом значении 74. Если значение велико, система стабильна только при 74 достаточно малых или достаточно больших значениях, что согласуется с результатом, полученным в Примере 3.8.
Если –∞ <oo, это уравнение соответствует поверхности S. Некоторые из них показаны на рисунке. 3.22, б. Когда коэффициент изменяется, когда точка в пространстве коэффициентов попадает на поверхность S, корень характеристического уравнения также изменяется и падает на мнимую ось. Поверхность 5 делит пространство коэффициентов на области. Каждая точка в области соответствует определенному равному количеству правого и левого корней. Эти области представляют D (м). Где м
Уравнение Тикаля. Разделение пространства коэффициентов на области с одинаковым числом правых корней в каждой области и назначение стабильных областей среди полученных областей называется методом D-деления. Характеристическое кубическое уравнение в пространстве коэффициентов может очертить четыре области: D (3), D (2), 0 (1), D (0). Последняя область D (0) является стабильной областью. Меняются не все коэффициенты, и для некоторых из них, например, для двух a1 и a2, использующих al -const, вместо поверхности вы получите линию. Это поверхностный разрез плоскости я8 = const.
Эта линия делит плоскость с коэффициентами _2 ± T и h- на области с одинаковым количеством правых корней (рис. 3.23). Для уравнений более высокого порядка (π> 3) вместо обычного трехмерного пространства вы получаете многомерное пространство и гиперповерхность, которая делит это пространство на области. Это делает задачу очень сложной и теряет внимание. Переходы через разбиение коэффициента D границ раздела соответствуют корневым переходам характеристического уравнения через мнимую ось, поэтому в общем случае D граничных уравнений разбиения D (/ o>) = (/ o) «+ i, (/ o)» — 1 + ••• + aa = 0. (3,79) (3.79) показывает, что при замене p- / co уравнение для границы разложения D может быть получено из характеристического уравнения системы.
Границы D-разложения могут быть построены не только в пространстве коэффициента характеристического уравнения R /, но также в пространстве параметров системы (постоянная времени, коэффициент усиления и т. Д.), От которых зависит коэффициент характеристического уравнения. a3 = const D раздел с одним (комплексным) параметром. Предположим, нам нужно изучить влияние на стабильность параметра v, который линейно входит в характеристическое уравнение. Для этого сначала характеристическое уравнение (3,80) D (p) = .S (/?) — F-WV (p) = 0, Где S (p) — многочлен, не зависящий от v. N (p) — многочлен с v факторами. D границы раздела определяются уравнениями 0 (/ a>) = 5 (/ ‘u) + viV (/ ©) = 0, (3,81) Откуда 7 = -5 (/ ©) / # (/ co) = A (co) / K (co). (3,82)
Поскольку параметр линейной системной переменной v — это не комплексное число, а действительное число (усиление, постоянная времени и т. Д.), Необходимо добавить условие Y ((o) = 0 в (3.82), но сделать это в исходной конфигурации. , Временно рассматривайте параметр переменной как комплексное значение v и пометьте его столбцом выше, чтобы отличить его от фактического значения v. При заданном значении от -oo до oo X (o)) и f (co) могут быть вычислены до (3.82), а граница D-разложения может быть построена на комплексной плоскости v. 5) R UM * Рисунок 3.24. При построении границ раздела D достаточно построить его для положительных значений (а затем дополнить его зеркальным отображением графика, построенного для действительной оси (рис. 3.24, б)).
Если o> меняется с -oo на oo в плоскости маршрута, перемещается вдоль воображаемой оси и заштриховывается с левой стороны (рис. 3.24, а), то такое движение в плоскости v происходит слева по объездной дороге. Измените, чтобы приспособить движение вдоль границ заштрихованного разложения D (замените o на -oo (рис. 3.24, б)) Если плоскость v пересекает границу раздела D в направлении штриховки (стрелка /), один из корней проходит от правой полуплоскости к левой в плоскости корня. Если плоскость o пересекает границу раздела D для штриховки (стрелка 2), в плоскости корней один из корней проходит из левой полуплоскости вправо. Если штриховка двойная (например, пересечение кривых), два маршрута пересекают виртуальную ось.
Чтобы определить область D (m), в частности область стабильности D (0), достаточно знать распределение корней любого произвольного значения (т. Е. Количество левого и правого корней). M v = vd. Передав плоскость vot этого параметра другим, значение D (m) в других точках можно определить по количеству пересечений, направлению и числу штрихов границы раздела D. Кандидативные стабильные области — это те, которые имеют штриховки внутри, поэтому они соответствуют области с наиболее левыми корнями. Чтобы проверить, является ли эта область на самом деле стабильной, вам нужно установить значение v0 в этой области. Sub
После того, как вы вставите vq в характеристическое уравнение, вы должны использовать любой критерий устойчивости, чтобы проверить, все ли корни характеристического уравнения левши. В этом случае, если все корни остаются, стабильной области нет. Другими словами, изменение только параметра v не может стабилизировать систему. Поскольку параметр переменной является действительным числом, из полученной стабильной области выбираются только стабильные сегменты. То есть сегмент действительной оси, который находится в стабильной области, например, сегмент A B 3.24, b на фиг.
Буду раздел с двумя параметрами. На практике часто необходимо найти упор на устойчивость двух параметров, которые линейно попадают в характеристическое уравнение замкнутой системы, а не одного параметра. D (p) = vW (p) -b, M (p) + L (p) = 0, (3.83) Где N (p)% M (p), Cp) — многочлен от p. v и q — переменные параметры, и нас интересует их стабильность. Подставив p- / co в (3.83), чтобы получить уравнение для границы D-разложения на плоскости параметров. D (fco) = v / v (fco) + мкМ (fco) -L (fco) = 0. (3.84) Введены следующие обозначения. N (fco) = N, (co) H-, N2 (co), M (fco) = fI, (co) + / Ma (co), (3 85) L (/ co) = L, (co) -H iL2 (co)
Разделите (3.84) на два уравнения и сделайте действительную и мнимую части по отдельности равными нулю vWi (со) + {W, (со) + L, (со) = 0; (3,86) vW2 (со) + | iM2 (со) + L2 (со) = 0 (3,87) Решение системы уравнений (3.86) и (3.87) для v и ^ V = At / D, (3,88) 1 * = D2 / D, (3,89) N <((o) M, (со) -Основные детерминанты системы, (3.90) Где D = Л / 2 (со) М2 (со) — / -1 (о) Mj (со) -Ц (0)) 1212 (ω) • ^^, (ω) — (σ>) » 2 (ω) -L2 (ω) (3,9!) (3,92) D2 = -Системный закрытый идентификатор. Так как W2 (co), M2M и 22 (co) — нечетные функции от ω, D, At и D2 — также нечетные функции от co, а v и µ — четные функции от co.
Смотрите также:
Примеры решения задач по теории автоматического управления

