Оглавление:




Построение эпюр внутренних усилий для стержня с ломаной осью
- Внутренняя силовая схема Для прутков со сломанными осями При проектировании станка часто приходится рассчитывать балку, ось которой представляет собой пространственную линию, состоящую из прямых отрезков. Например, на рисунке. 298 показана балка,
состоящая из трех стержней AB, BC и CO. Первые два стержня находятся в одной плоскости, а остальные стержни расположены в плоскости, перпендикулярной первому. Расчет такого стержня начинается с определения коэффициента внутренней
силы в нескольких сечениях. Коэффициент силы N. Для нахождения Людмила Фирмаль
наиболее сильного (опасного) участка поперечного сечения u, MH,<2U будут построены , 345 первоначально каждому стержню должна быть присвоена ось. Обычно ось, совпадающая с осью балки, указывает на ось Oh, остальные две оси совмещены с осью инерции секции. График момента и боковых сил каждого стержня строится в виде плоского бруска, используя правила ранее принятого знака(в случае момента) (344 мы мысленно ставим каждый стержень по отношению к себе, так что линия визирования направлена в начало координат от положительной оси z (в случае графика и поперечных сил)). Рассмотрим пример построения графика для бара, как показано на
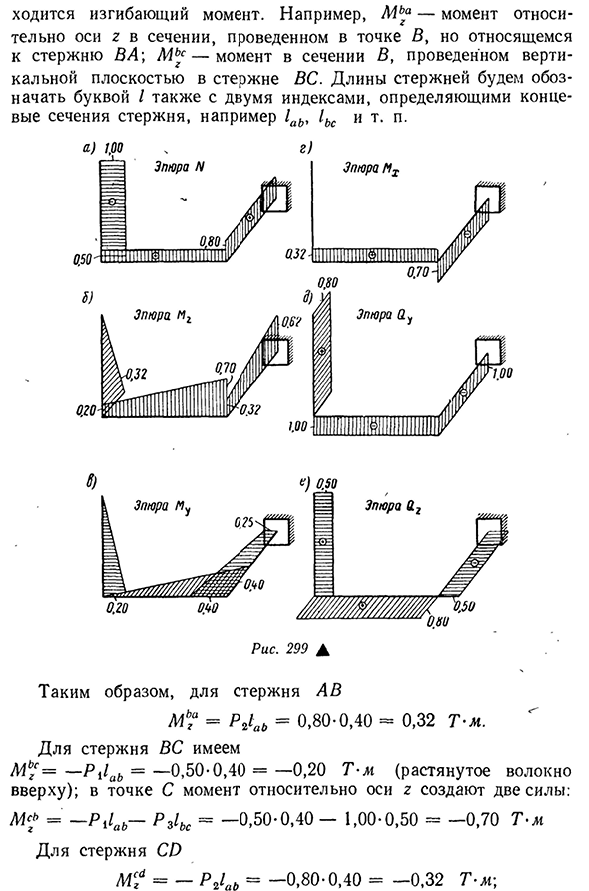
рисунке. 298 когда на него действуют три силы: Р4=0,50 Г; P2=0.80 T и P3=1.00 T на рисунке. 299 показаны графики вертикальной силы IV, изгибающих моментов m g и y m, крутящего момента MX и боковых сил F5 и 0_g. эти графики основаны на расчетных вертикальных значениях сечений на концах каждого стержня. Если посмотреть на отрезную часть со стороны секции, то получается, что MX стремится повернуть секцию по часовой стрелке, крутящий момент считается
- положительным. Сюжет нормальной силы наиболее просто составляет N.To для этого необходимо спроецировать все силы на ось соответствующего стержня и определить силу N по формуле EX=0. 299, а. Изгибающий момент несколько трудно определить. Рассмотрим расчет изгибающего момента mg более подробно. В стержне а с изгибом относительно оси g возникает только одна сила Р2, поэтому график момента имеет форму треугольника. Один из них относится к вертикальному стержню,а другой-к горизонтальному. Индекс на
первом показывает точку, в которой нарисовано сечение,и два индекса вместе определяют стержень- 346 изгибающих моментов. Например, момент Mga для оси g в сечении, удерживаемом в точке B, связан со стержнем VA\mga моментом сечения b, а длина вертикальной плоскости стержня BC обозначается двумя индексами, определяющими конец стержня, например, 1C. Рис 299а
Таким образом, стержень «M b» =P21A=0.80-0.40=0.32 т-м. Для терминала у нас есть М г С= — П\1А=—0,50-0,40 — -0,20 создать двух сил на данный Людмила Фирмаль
момент точки C относительно оси г.=- Р^1А-P31C= —0,50-0,40 — 1,00-0,50 = -0,70 т-м для СВ м род? = — P21A= — 0.80-0.40=-0.32 т-м- £ 347M г C= — R21a-R31sa= —0,8-0,4 — 1,00-0,30 = — 0,62 т-м Согласно этим данным, график mg показывает это на рисунке. 299, б. Аналогично построен участок m u (рис. 299, в). Крутящий момент вычисляется более легко. Крутящий момент стержня AB равен нулю в центре Солнца М * ы=р последовательно пронумерованы g1a1>=0.32 т-м, И в баре М? = «Р Rz1c=-0,7 0т-м. По этим данным строится график крутящего момента (рис. 299, г). Боковая сила определяется как сумма проекций оси y и 2 всех сил, действующих на отрезанную часть. В соответствии с
правилами, принятыми выше, боковая сила в стержне найдена, и график показан на рисунке. 299, д и Е. В зависимости от размера и формы сечения каждого элемента балки по формуле (а), приведенной в предыдущем пункте, нормальное напряжение данного сечения и полное тангенциальное напряжение с участка о могут быть определены не только из момента M x, но и из двух поперечных сил 0 u и FG, которые должны быть получены по формул
Смотрите также:
| Понятие о расчете коротких балок, лежащих на сплошном упругом основании. метод начальных параметров | Косой изгиб |
| Сложное сопротивление общие понятия | Одновременное действие изгиба и продольной силы |

