Оглавление:







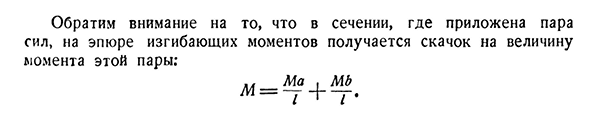

Построение эпюр изгибающих моментов и поперечных сил
- График изгибающих моментов и боковых сил. П р и М плат ep43. Постройте график момента и боковых сил балки, находящихся на двух опорах и силы Р(рис. 159). Чтобы вычислить M и Q в любой части этого луча, вы должны сначала найти реакцию. Как использовать 159 предполагаемое направление этих реакций D, Na, B. Из условия, что сумма проекций всех сил на ось балки равна нулю, получаем ее [72]рис. 233 изгибающего момента и поперечных сил Этот результат можно предсказать заранее, так как нагрузка
перпендикулярна оси балки. Сделать сумма моментов силы по отношению к точке s, мы получим: И Точно так же И £Ма=0; — В1 — \ — РА = Б Для проверки правильности полученных результатов суммируем проекцию всех сил на вертикальную ось: _u: A-P-j-B=0, или A — \ — B-R. Если мы подставим значение найденной реакции、: ПБ ТП a_P(а+б) р я я я Это соответствует условиям равновесия. Такие проверки должны проводиться всегда, так как ошибки в определении реакции неизбежно приводят к ошибкам в построении участков Q и M. Для получения уравнения, дающего значение поперечной силы и изгибающего момента в любом сечении балки, центроид с
ечения 7-7 между точкой А и точкой С на расстоянии Xi от конца а показан Людмила Фирмаль
через Oh. Для расчета боковой силы Q в этом сечении удобнее рассматривать левую отрезную часть, так как она имеет меньшую силу (только силу L). Принимая во внимание часть балки на левой Луе, сложим внешние силы балки и получим формулу поперечного расстояния x x от опоры A.:. RY Сверху сечение oh и перпендикулярно оси силы Qi в проектном сечении (1 2. 6) прочность на изгиб[CH, 234 испытание. ДВЕНАДЦАТЫЙ Боковая сила в поперечном сечении с осью абсцисс не зависит от этого расстояния. Таким образом, пока x t изменяется между 0 и a, боковые силы остаются постоянными, и участок на этом участке представлен прямой линией F^D^,
параллельной абсциссе 159). Формула Qj(12.6) справедлива до тех пор, пока сечение, которое мы взяли, не проходит через точку C, т. е. O^X j^a. таким образом, сумма проекций сил, приложенных к левой части срезаемой балки, изменяется. Чтобы найти величину боковой силы во втором сечении, нужно взять другое сечение между точками B и C с центром тяжести O2. Его расстояние x2 отсчитывается прямо от опоры B. В этом случае выгоднее рассмотреть правильную часть балки, так как на нее воздействует только сила В. С учетом правой
- отрезной части балки получаем формулу поперечной силы сечения 2-2: Знак минус берется, так как сила B, приложенная к правой отрезной части, направлена вверх. Учитывая обрезанную часть с левой стороны, легко увидеть, что она будет иметь то же значение, что и Q=A-P—B (A-~B=P). Выражение (12.7) указывает, что оно подходит для любого значения x2, которое не превышает раздела 5, т. е. 0^x2^/>, и не зависит от x2. График боковых сил второго сечения представляет собой прямую линию eB)в абсолютном значении этого примера равна ФОМ топор/я —— — • Опасность по отношению к касательным напряжениям лежит во всех сечениях балки SV сечения, а для построения изгибающего момента, такого же сечения в левой части балки. Рассматривая левую отрезную часть, она
находится в сечении/-/как сумма моментов силы, приложенных к центроиду сечения.: Лл л бл DC=D * jTj= — * jq, Значение момента (12.8) А MX-это функция первой степени, и поэтому, если мы переместим наш участок, изменим x, он изменится по закону прямой линии. Полученное выражение MX (12.8) подходит до тех пор, пока сечение не проходит через точку C, то есть до 0XX A. Как только Xi станет больше AU в левой части луча, вы уже получите две силы: D и R, и Формула (12.8) будет непригодна. Поскольку этот график является прямой линией, x{достаточно дать только два значения, чтобы получить две точки графика момента. В X g=0=0-это ордината под точкой D, аналогично в La I Bab~x x=a вы получаете ординату
под сечением C, LT A=-]—— При построении графика мы соглашаемся проставить положительную вертикальную ось (по направлению Людмила Фирмаль
к положительной оси y) и отрицательную. Иногда принимается и обратное расположение системы координат, что часто практикуется при расчете кадров. Помимо оси Х вверх(положительный момент! Отрезок CiDi выражает вертикальную координату на шкале и соединяет линию с точкой Di, Мы получаем первый участок графика момента. Чтобы построить график второго сечения, проверим выражение moment236 прочность на изгиб[CH. ДВЕНАДЦАТЫЙ Усилие, приложенное к правой части отрезной балки против точки O2: (12.9) Мы рассмотрели правую часть, и сила b повернула ее против часовой стрелки против точки O2, так что оказалось, что момент был положительным в этой области. Полученная формула(12.9) представляет собой уравнение прямой, подходящее для O x2B. At=B, TI2=4-и x2=0, TI2=0. Таким образом, вторая
часть графика момента рисуется прямо поперек балки-изгибающий момент, который положителен и достигает максимума в сечении С-это то же самое. M p A x=^. (12.10)) В этом разделе есть максимальное нормальное напряжение. A=B= — ^(сила приложена к середине пролета): Лл-р л Д’Макс•(12.10′) Рассмотрим несколько примеров графиков для различных типов нагрузок на балку. П р и М EP44. График момента и поперечной балки показан на рисунке. 161 с этого луча Сила M и Q на крайнем правом свободна, но при построении участка, всегда принимая во внимание правильную часть луча, это можно сделать без предварительного определения опорной реакции. Если вы возьмете участок первой секции между точками C и B,
вы можете увидеть, что сила не действует на правую сторону остальной части OjB. Таким образом, изгибающий момент Oh и боковая сила в поперечном сечении равны M и оси Поперечное сечение Q горизонтальной оси. Для < 2=+л Ноль это относится между b и C. Сюжет показан на рисунке. 161; ■ Mdpp== Из них P (1-a)и Qmax=P72] фигуры изгибающего момента и поперечной силы 237 М без силы Заметим, что в этом пучке мы построили определение графика Q и реакции поддержки. П р и М плата ep45. График момента и поперечной балки показан на рисунке. 162, нагружая непрерывную равномерную распределенную нагрузку прочности^(представленную кг1м, т1мп и др. да что с тобой такое? Здесь вам нужно начать с определения реакции поддержки. Реакция H равна нулю, а реакции 4 и B симметричны и равны; каждая из них равна половине
лежащего повсюду. Нагрузки на пучки: а=б=1л. Возьмите сечение O на расстоянии x от левого края балки. На него воздействует реакция А и равномерно распределенная по длине х нагрузка q. Для определения поперечной силы в поперечном сечении необходимо взять сумму сил, приложенных к левой стороне отрезной части балки. С левой стороны сечение направлено вниз, равное силе a=~, вверх, и в результате равномерно распределенных нагрузок расположено по длине x, qx. Так М-А-Ц= — ц. Сдвиговая сила изменяется с изменением x по прямому закону iinii для построения дают два значения переменной x: при x=0Q= — ^и x-l Q-график поперечных сил рис. 162; maxQ=Y. Чтобы построить график м, составьте сумму моментов одинаковой силы, приложенной
к рассматриваемой части балки относительно точки О. Имейте в виду, что полученное qx прикладывается к центру отрезка длины x, а плечо к точке O равно получить: m—4-Ah-qx y=x — =C — = {I-x). Это уравнение подходит для расчета изгибающего момента любой балки.238 подтверждение прочности на изгиб[Глава II. В этом случае величина изгибающего момента зависит от квадрата абсциссы x, поэтому контур участка представляет собой криволинейно-квадратную параболу. Чтобы построить эту кривую, мы наметим по крайней мере три или четыре ее точки. Имеем: h=O M=0; M_3^2. 4/32′ * h=^L1= 4 — 4 ) = + 4; » x-1 714=0. Сюжет момента получает форму, показанную на рисунке. Сто шестьдесят два Чтобы найти L4, найдите абсциссу x0 соответствующего сечения и обнулите производную L4 с x\ д М ql2qxQ н д х-2 2′ Где X0=4 и^max=+^G -^)=+$. (12.11)
максимальный изгибающий момент возникает в середине пролета, то есть в сечении Q=0, что является результатом приведенного выше (§ 71) соотношения между M(x)и Q (x).
Смотрите также:

