Оглавление:




Построение эпюр для криволинейных стержней
- Структурная схема для изогнутого стержня В поперечном сечении плоской изогнутой балки, как и в каркасе, чаще всего действуют три коэффициента внутренних сил (N, Q, M), а ось имеет дело со стержнем, очерченным дугой окружности.<п), м (СР) Если взять правило 66 / V и Q нормальных знаков (см.§ 15 и 19), то M строится
на сжатом волокне, как каркас. В качестве примера рассмотрим плоскую криволинейную балку. 79, авг. Для любого раздела C запишите значения N (f), Q(f) и M(f). Чтобы получить N (f), нужно заставить P и P2 спроецировать направление оси стержня в точке C. Для облегчения конструкции их можно мысленно перенести в точку C(рис. 79,и они обозначены пунктирной линией).
Тогда N (f)=Pi cos f-B P2sin f. Для получения Q (f) необходимо приложить Людмила Фирмаль
усилие, приложенное к детали AC9, к плоскости, т. е. к направлению сечения OS: Q (f)=Pi sin f-P2cos F. Мы согласны рассматривать изгибающий момент как положительное значение при построении выражения для изгибающего момента в любом поперечном сечении, например, когда он вызывает сжатие волокон внутри стержня (т. е. увеличение кривизны стержня). Пусть M (f)=Pt. Объявление-Р2 * КД =
ПТР(1-соѕ Ф) — p2r грех Ф. Полученная формула позволяет построить графики Nt Q и L4. Предполагая, что Pt P и P2 равны 0.5 p, N (f)=(cos f+0.5 sin f) P; Q (f)=(sin f-0.5 cos f) P; (3.9) M (f)=(1-cos F—0.5 sin f) PR. Рассчитайте значения N, Q, M в нескольких разделах (таблицах). 3). Обозначив ось стержня под углом 10°, откладываем шкалу нормалей к соответствующим осям (радиусам) — Q, N (положительный-выход,
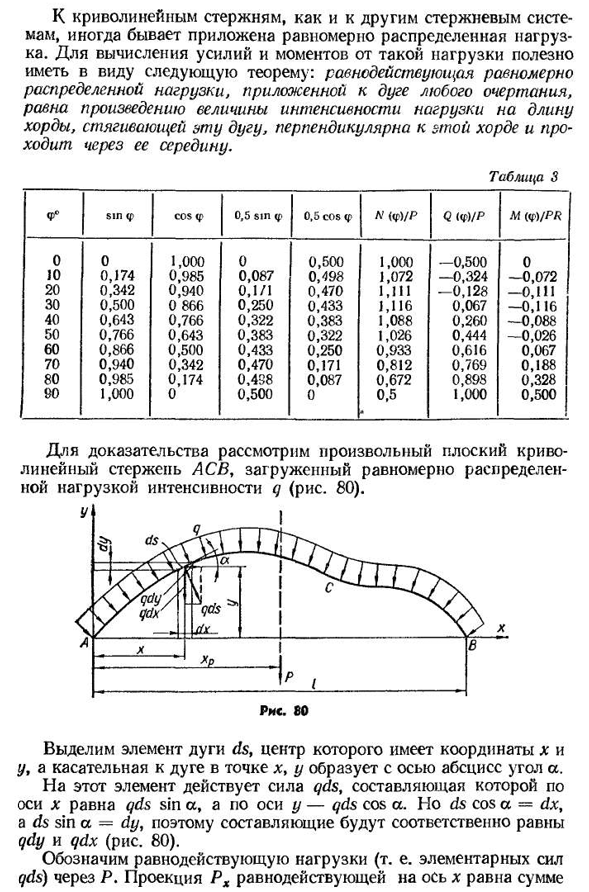
- отрицательный-вход) и M (на сжатом волокне), соединяя продольные оси ребрами плавных кривых (79, б). Рассмотрим общий вопрос о сюжете изогнутой палки. Три.* 67 изогнутые стержни, как и другие стержневые системы, иногда имеют равномерно распределенные нагрузки, приложенные к ним. Результат равномерно распределенных нагрузок, приложенных к дуге произвольной формы, равен произведению силы нагрузки на длину хорды, которая тянет эту дугу и перпендикулярна этой хорде. Таблица 3 ФО грех, потому
что Ф ф0. 5 грех f0. 5 cos f L’(f) / R<2(f) / R (f) / R/? Ноль. 0 1,000 0 0,500 1,000-0,500 0 10 0,174 0,985 0,087 0,498 1,072-0,324-0,0,072 20 0,342 0,940 0,1/1 0,470 1,111 −0,128 −0,111 30 0,500 0 866 0,250 0,433 1,116 0,067-0,116 40 0,643 0,766 0,322 0,383 1,088 0,260-0,088 50 0,766 0,643 0,383 0,322 1,026 0,444 −0,0 2 6 60 0.866 0.500 0.433 0.250 0.933 0.616 0.067 70 0.940 0.342 0.470 0.171 0.812 0.769 0.188 80 0.985 0.174 0.438 0.087 0.672 0.898 0.328 90 1000 0,5 0,500 0 0 • 1,000 0,500 Четыре. Для доказательства рассмотрим произвольный плоский криволинейный стержень с равномерно распределенной нагрузкой на прочность q (рис. 80). Выделите элементы дуги ds, центры которых имеют координаты x и y, а касательная дуги в точке x, y образует ось абсцисс в виде а.
На этот элемент воздействует сила yds и сила y-QDs cos a, составляющая Людмила Фирмаль
которой на оси x равна qds sin A. 80). Проекция результата px на ось X равна сумме Qdy всего, т. е. 68geroections основной силы qds: О РХ=, Ф Qdy-м\ды-м\ды=0. ACB A6 Аналогично, мы находим, что результирующая проекция на ось y равна I Ru=qdx=q\dx=q dx=QL. А6 АСВ Таким образом, в результате То есть она равна произведению силы нагрузки на длину шнура/, затянутого дугой переменного тока V. Поскольку Px=0, результат перпендикулярен строке, поскольку ось x, или ось k, ориентирована вдоль строки. Затем вычисляем сумму моментов фундаментальных сил относительно начала координат: Вопрос: у вас есть какие-либо вопросы? Значения
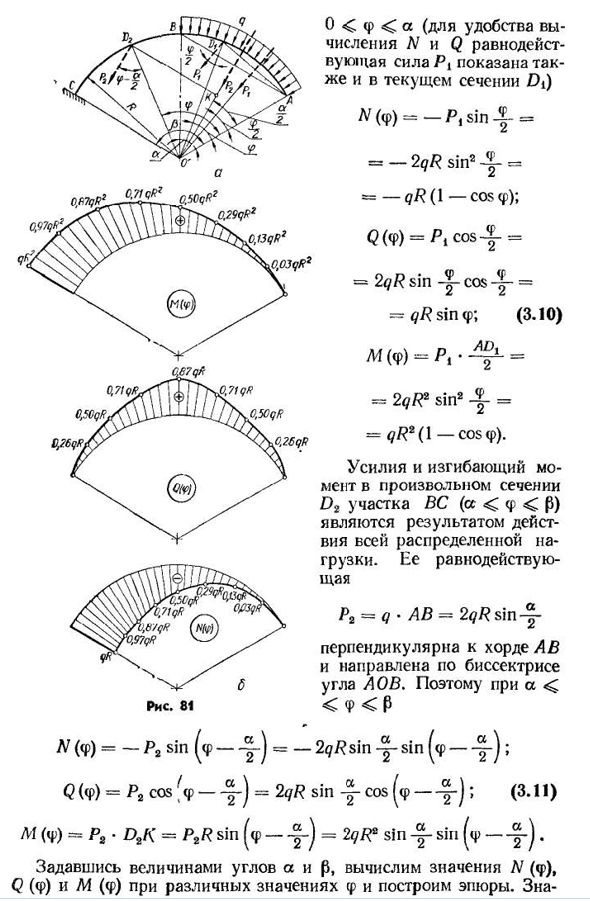
i0 вопрос-вопрос ыды = 6, 6, 6 Результирующая рука относительно начала координат равна xr. Тогда, согласно полученной теореме RXR=^M d или QL•kr=moment, xr==означает, что результат проходит через середину хорды. Теорема доказана. Чтобы проиллюстрировать применение этой теоремы, рассмотрим следующий пример: Найдем формулу для изгибающего момента, как поперечной, так и продольной силы в поперечном сечении кругового криволинейного стержня(рис. 81, а), AB равномерно распределенная нагрузка, нагруженная по частям (заданные значения q, R t a и p). При этом изогнутый стержень имеет два сечения-AB и BC. Для любого участка сечения AB (0<;(3.10)м(ф)=р г-Ф — = = 2qR2sin2= = qR2(1-с COS<Р). Сила и изгибающий момент любого сечения D2 солнечного сечения
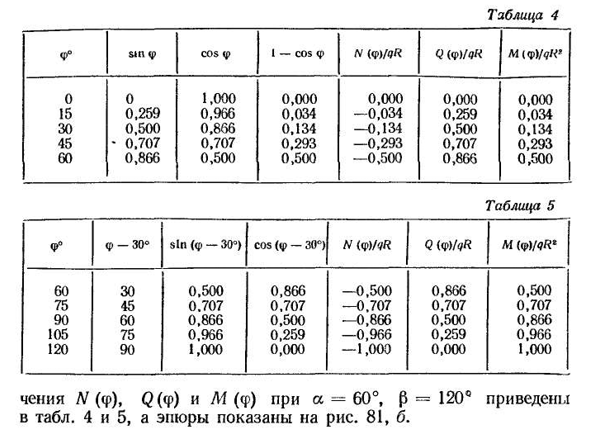
(a<f<p)являются результатом действия всей распределенной нагрузки. Результат P2-q * AB=2qRsin-перпендикуляр к хорде AB, ориентированный по биссектрисе угла AA. Таким образом,<<Ф<P2qR грех грехом (<п — ; ( < !да что с тобой такое? Q (<f)=Pi cos% — = 2qR sin-J-cos; (3.11) M (f) = Ps•D2K=P2R sin (f-y -) =2qR2sin-J-sin учитывая значения углов a и p, значение знания N (<p), Q (f), M (f) и M (f), в различных значениях построения с f (<p- Таблица 4 ф°ф грех, потому что Ф1-это потому, что Ф Н ц ш МКР М(ф) / <нет Ноль. 0, 1,000, 0.000, 0.000, 0.000, 0.000. 15 0,259 0,966 0,034-0,034 0,259 0,034 30 0,500 0,866 0,500-0,134 0,134 45 • 0,707 0,707 0,293 −0,293 0,707 0,293 60 0,866 0,866
0,500 0,500-0,500 0,500 Таблица 5 F°F-30°sin (f-30°) COS (f-30°) (f)/ ’ L? Вопрос(<&)/<}&м(ф)/<?Я 60 30 0,500 0,866 0,866 0,500-0,500 75 45 0.707 0.707-0.707 0.707 0.707 90 60 0.866 0.500-0.866 0.500 0.866 105 75 0,966 0,259-0,966 0,259 0,966 120 90 1,000 0,000 — 1,000 0,000 1,000 Значения N (CP), Q (<p)и L1 (<p)=60°、£==120°значения приведены в таблице. На рисунке 4 и рисунке 5 показаны. 81, б.
Смотрите также:

