Оглавление:
Построение доверительных интервалов для трендов, приводимых к линейному
Процедура построения доверительных интервалов полностью переносится и на случаи, когда уравнение кривой может быть после некоторых преобразований сведено к линейному тренду. Оценивание параметров преобразованных уравнений, как было указано ранее, осуществляется методом наименьших квадратов.
В практике криволинейного выравнивания широко распространены два вида преобразований: логарифмирование и обратное преобразование 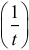 . При этом возможно преобразование как зависимой переменной
. При этом возможно преобразование как зависимой переменной 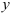 , так и независимой
, так и независимой 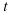 или одновременно той и другой.
или одновременно той и другой.
Рассмотрим процедуру построения доверительного интервала прогноза для модифицированной экспоненты
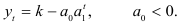
Прологарифмировав уравнение, получим линейную функцию от 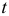 :
:
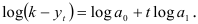
Пусть асимптота 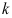 задана, т.е.
задана, т.е. 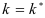 и не содержит ошибки. Обозначим
и не содержит ошибки. Обозначим
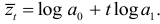
Тогда доверительный интервал прогноза для модифицированной экспоненты будет определяться как доверительный интервал (9.3) для прямой, т.е.
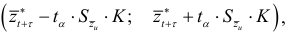
где 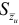 — среднее квадратичное отклонение от тренда
— среднее квадратичное отклонение от тренда 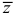 . Зная границы доверительного интервала для
. Зная границы доверительного интервала для 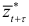 , легко определить доверительные границы прогноза для
, легко определить доверительные границы прогноза для 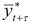 :
:
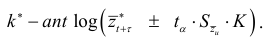
Так как экспоненциальная кривая 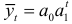 логарифмированием преобразуется к виду
логарифмированием преобразуется к виду 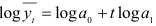 , то доверительный интервал прогноза имеет вид
, то доверительный интервал прогноза имеет вид
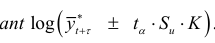
В доверительных интервалах (9.4) и (9.5)
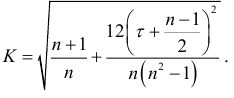
Пример 9.3.
В табл. 9.3 дан динамический ряд, характеризующий объем продаж.
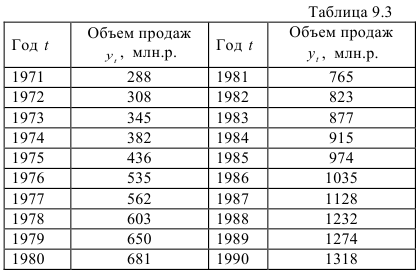
Для выбора функции тренда применим метод характеристик. Построив графики скользящих средних приростов и их характеристик, сделаем вывод о том, что тренд описывается показательной функцией
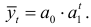
Прологарифмировав уравнение, получим прямую
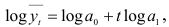
оценку параметров которой осуществим методом наименьших квадратов. Итак, наилучшей функцией, характеризующей объем продаж, является функция
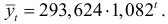
Для построения доверительного интервала прогноза вычислим прежде всего среднее квадратичное отклонение:
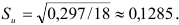
Используя формулу (9.5), строим доверительные интервалы прогноза для периода упреждения:
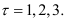
Значения коэффициента 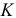 будут равны соответственно:
будут равны соответственно:
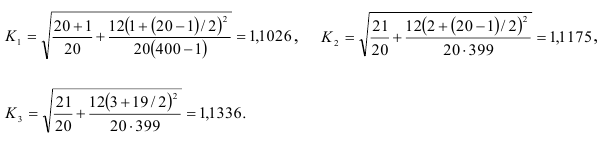
Значение квантиля 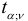 , взятое из таблицы распределения Стьюдента при заданном уровне значимости
, взятое из таблицы распределения Стьюдента при заданном уровне значимости 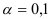 и
и 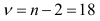 степенях свободны, равно
степенях свободны, равно 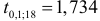 . Вычислим для
. Вычислим для 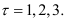 значения
значения 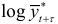 :
:
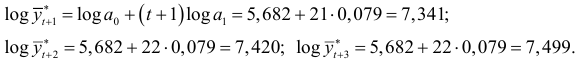
Тогда доверительные интервалы, для 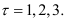 будут иметь вид:
будут иметь вид:

Прогноз для 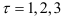 составит соответственно: 1508,09, 1636,069 , 1807,373. Вычисленные значения прогноза принадлежат соответствующим доверительным интервалам.
составит соответственно: 1508,09, 1636,069 , 1807,373. Вычисленные значения прогноза принадлежат соответствующим доверительным интервалам.
Отметим еще раз, что процедура разработки прогноза с использованием аналитического выравнивания тренда состоит из предварительного выбора одной или нескольких кривых, которые наилучшим образом соответствуют характеру изменения ряда динамики, оценки параметров выбранных кривых, проверки их адекватности прогнозируемому процессу, окончательного выбора кривой роста и вычисления точечного и интервального прогнозов.
Эта лекция взята со страницы предмета «Эконометрика»
Предмет эконометрика: полный курс лекций
Эти страницы возможно вам будут полезны:

