Оглавление:














Последние достижения в теории теплообмена при турбулентном режиме движения
- Возможность совершенствования расчета турбулентного теплообмена основана на наилучшем знании механизмов турбулентности. Полное описание такого потока всегда Чтобы воспользоваться преимуществами флуктуирующей природы, необходимо иметь знание параметров потока (скорости и давления) в каждой точке потока и в каждом moment. It в настоящее время он недоступен. Поэтому такое утверждение должно удовлетворяться знанием среднего времени. Процесс преобразования уравнения Навье-Стокса был завершен в 1883 году в o.
Он был объяснен Рейнольдсом. Параметр мгновенного потока описывается как сумма среднего значения времени (обозначенного тире над буквой) и мгновенного отклонения (вариации) от этого значения Прайм) : у = у — {- ИИ ’ у = в ^ — ВФ; п = п + ПФ. (8-19) теперь введем эти выражения в уравнение Навье-Стокса (6-14). Это среднее значение всех временных колебаний. «=0 согласно определению; g? ’=0; p ’= 0 (но произведение u’ и т. , не обязательно должен быть равен нулю), для устойчивого течения он выглядит так:- di, di. — Ди др 。 Чи г + * гг) = — / нет ДГИ. ?2₄ / ’Ду’2, Ди «ручьи» .ду ’западной долготы’, ₀ + *1Вт + ^2+ Д ?7-CH CH’E^ + — 5Г+ — ^Л ⁽ ⁽ 2 compatible совместим с 2 Уравнения V и w .
Энергия, необходимая для фазового перехода единицы массы вещества, называется удельной теплотой фазового превращения. Людмила Фирмаль
Мы также обнаружили, что уравнение неразрывности не меняет своего вида, если оно описывается значением di, усредненным по времени .Ди ДГ л ДХ 1 Уравнение для пограничного слоя в среднем времени Oy’DZ принимает следующий вид, согласно упрощению пограничного слоя в Прандтле: Уравнения пограничного слоя по существу описывают тот же самый турбулентный процесс обмена, который уже описан в разделе 8-1 .Мгновенный массовый поток, перпендикулярный направлению Существует pt /для каждой единицы времени и единицы площади основного потока, а x-передача импульса, связанного с этим потоком, -pt / u ’ .
Это усредненный срок、 Еще одно выражение фрикционного stress .It выражается в Формуле (8-2) .Полное уравнение Навье-Стокса содержит несколько таких членов (представляющих движение величин 3-способ перемещения координатных осей) .Уравнения (8-20) и (8-21) позволяют лучше понять процессы, вызывающие турбулентные напряжения трения .Для интеграции Для уравнения необходимо использовать дополнительную формулу, которая соединяет термины, содержащие значения переменных (и»2, u’V»и т . д.) к средней по времени сумме .
Т .к .В . Буссинеск Первым, кто предложил такое выражение, представив формулу для напряжения трения в турбулентной области, является^ = — p (^ ’) =peₘg — .(8-22) термин ЭМ называется коэффициентом Турбулентность кинематическая viscosity .It можно видеть, что приведенная выше формула очень полезна в отношении теплопередачи calculations .In порядок расчета поля потока、 Это очень удобно, потому что экспериментально было выяснено, что именно от сложности зависит скорость .Основываясь на нескольких концепциях теплообмена в турбулентном режиме, Прандтль Оказывается, что соотношение di di du du (8-23) (вертикальная линия указывает, что напряжение трения имеет тот же знак, что и градиент скорости), и они относительно просты.
Формула для длины перемешивания I (например, пропорциональная расстоянию от стенки) хорошо согласуется с экспериментальными данными .Формула (8-23) используется в качестве основы для многих расчетов Поток .Таким же выражением в подобных рассуждениях стал и т .Кальман .такие значения, как u ’2, u’v’, измерялись с помощью термоанемометра для различных типов потоков .Также рассматривать Статистическая теория турбулентности .Окей .L с применением к уравнению энергии уравнения Рейнольдса (7-3) .Упрощение теории пограничного слоя, сделанное Прандтлем.
Скорость распространения энергии пограничного слоя в турбулентном режиме со средним временем по следующему уравнению:/ — dt, — dt .dh d (u’t’) (8-24) это Уравнение снова отличается в зависимости от соответствующего уравнения установившегося ламинарного течения и последнего члена справа, представляющего теплообмен при турбулентном течении .Режим, эквивалентный уравнению (8-1) .Буссинеска вводится в этот тепловой поток в турбулентной области и уравнение 4 -= -, (8-25) eq называется Турбулентная теплопроводность эта формула, наряду с формулой (8-22), очень важна для расчета теплопередачи по характеристикам потока .
Самое простое предположение о соотношении eₘ/, то есть всегда получается результат, который полностью совпадает с экспериментальным data .It-это еще проще .Предположим, что eₘ / eQ = L .Это, как вы сразу увидите, соответствует аналогиям Рейнольдса .За последние несколько лет было опубликовано много статей、 Теплопередача различных типов турбулентности, основанная на аналогии Рейнольдса, или более общей формулировке соотношения 2 факторов турбулентности Вы также можете передавать файлы с Вашего компьютера на ваш компьютер .computer .In в этом разделе мы опишем основную идею всех этих расчетов в общих чертах, а также более подробно проанализируем методы, предложенные Kalman .In случай ламинарного течения.
Изменение скорости и температуры в направлении, перпендикулярном потоку, значительно больше, чем изменение скорости и температуры в направлении, параллельном потоку, уравнение Напряжение трения и тепловой поток описаны на стр . 253 .Эти соотношения можно записать в следующем виде: (8-26) -DT v qi ~~~ l — dy〜 * Pr’pf_rf7 (8-27) уравнение — (8-28) (8-29) размер времени-напряжение трения и тепловой поток, связанные с турбулентным обменом, могут быть описаны в соответствии с (8-22) и (8-25) du qt〜 ‘dy’ .t можно интерпретировать как среднее значение значений .
2 параметра имеют те же значения, что и Кинематическая вязкость v и называются коэффициентами турбулентности вязкости и переноса Heat .It следует помнить, что эти параметры являются комплексной функцией расстояния от стенки, критерия Рейнольдса и др .variables .In аналогия Рейнольдса, коэффициенты являются Турбулентный перенос импульса (e^) и тепла (s^) были эквивалентны .Это легко увидеть, когда уравнение турбулентного теплового потока разбивается на уравнение напряжения трения .Режим турбулентности .Результат выглядит так: um’du * (8-30) e When =% ?Эта формула совпадает с формулой (8-3) .Однако данные последних экспериментов показывают, что их нельзя рассматривать Эти 2 коэффициента точно такие же .
По причинам, по которым связь, называемая критерием турбулентности Прандтля (Pr), скоро станет очевидной、 Величина потока пограничного слоя составляет около 0, 7, а величина следа и вихревого потока за закругленным объектом-около 0 .5 .Pr= -^ -* .。 (8-31) измерение Seij[L .120]и его сотрудниками * и Людвигом (L .121) критерий прандулярной турбулентности«не является постоянным, например、 Поток пограничного слоя имеет тип потока, он зависит от расстояния от стенки .Тем не менее, существует еще много расчетов, основанных на том, что критерий турбулентности Прандтля равен следующему: Единицы, и эти расчеты хорошо согласуются с реальностью .Использование опорных фигур турбулентности Прандтля создает небольшую трудность .
Из единицы, поскольку в определенных условиях течения это значение считается постоянным .Однако, когда кто-то пытается сделать критерии Прандтля переменной、 От расстояния до стены и других параметров весь расчет, основанный на аналогии Рейнольдса, теряет свою эффективность во многих случаях .ways .In раздел 8-1, подача Подслой становится полностью ламинарным или полностью турбулентным в ядре flow .In факт, самые последние измерения показывают что завихрение имеет специфическое Количество прямой турбулентности на самой поверхности .
Таким образом, как ламинарные, так и турбулентные потоки имеют трение одновременно, за которым следуют полное напряжение трения и тепловой поток Опишите в соответствии с формулами (8-21) и (8-24) следующим образом:- =+=+ (8-32) *в немецкой литературе Prₜ можно определить как: Метод: (э, э) пр .(8-33) g / v I dt Q-Qi + ^ t ^ «pt + Hy〜» используя первое из этих уравнений, коэффициент турбулентности вязкости e, n、 Как только поле потока становится известным .Затем можно ввести это значение в Формулу (8-33) и рассчитать температурное поле и тепловой поток .Уравнение импульса и Например, турбулентная энергия пограничного слоя (8-21) и (8-24) может быть записана в виде: (8-34) (8-35), когда поле скорости и поле давления известны из измерений.
Тогда первое из этих уравнений можно решить относительно неизвестного element .It получается как функция координат, а в некоторых случаях как критерий Рейнольдса .Это значение можно ввести следующим образом Если Pr / известен, решите 2-е уравнение относительно temperature .To чтобы получить коэффициент турбулентной вязкости с достаточной точностью, необходимо обладать очень точными знаниями .Потому что градиент компонента скорости должен быть рассчитан и введен в уравнение импульса .Поэтому формулы (8-32) и (8-33) обычно используются вместе Он предполагает изменение m и q вдоль координаты y .In в некоторых случаях напряжение трения известно .
Например, для совершенно стабилизированной подачи в трубе, баланс Это также указывает на то, что напряжение трения линейно возрастает с увеличением радиуса R .можно рассчитать коэффициент турбулентной вязкости es, используя уравнение (8-32), если: Кривые распределения напряжения трения xw и скорости стенок имеют вид known .In течение пограничного слоя, основные изменения скорости происходят вблизи стенки, за счет чего、 Напряжение трения существенно не изменяется при этом малом значении .Поэтому для пограничных слоев напряжение трения часто принимается постоянным .Перпендикулярно к surface .In в любом случае решение уравнения о 8м (8-32) дает формулу (8-36), по которой можно рассчитать коэффициент турбулентности .
Градиенты вязкости, напряжения трения и скорости известны, поскольку известны измеренные значения .Затем, если положение, где q-функция, является допустимым, определяется температурное поле .Расстояние от стены .Для потоков с пограничными слоями предположение о том, что q является постоянной величиной, может обеспечить разумную аппроксимацию фактического состояния .«Поток по каналу» или Хотя труба q сильно изменяется*по всему поперечному сечению, отношение q / x изменяется незначительно, но критерий Прандтля не так уж и мал (например, около 0, 1) .
- Воспользоваться этот факт, мы разделим уравнение (8-33) в уравнение (8-32) (в / пр) + (е» / пр) ДТ ду (8-37) 1Т .х постоянно равны qjxw и дают следующие зависимости для профиля температуры: ₜf 1С+ J 6 /Рг) + (W / PRᵣ) Odu .(8-38) расчет Интеграл коэффициента турбулентной вязкости et и уравнение (8-38) выполняются численно на основе измеренного профиля скорости, или, если известно, аналитически .Формула для анализа профиля скорости .Кальман делит весь профиль скорости на 3 слоя (ламинарный, буферный, турбулентный) .) 、 Получаем простую формулу для аналитических расчетов .
Уравнение, которое может объяснить размер этих 3 областей и поля скоростей каждой области показано на рисунке 5 .6-20 .In кроме того, Калман предположил, что член, содержащий коэффициент турбулентной вязкости, исчезает в уравнении, поскольку ламинарное течение в ламинарном подслое полностью ламинарно .(8-32) и (8-33) .С другой стороны, он предположил, что в турбулентном ядре турбулентная вязкость намного больше, чем ламинарная вязкость или термическая conductivity .So, согласно этому Он не рассматривал члены уравнений (8-32) и (8-33) .
Например, энергия, передаваемая в систему, где жидкая вода находится в равновесии со льдом при нуле градусов Цельсия, расходуется на плавление льда, но температура при этом остаётся постоянной, пока весь лёд не превратится в воду. Людмила Фирмаль
Они представляют собой ламинарные течения в турбулентности zone .In в буферном слое предполагалось, что течение постепенно изменяется от ламинарного к турбулентному Все члены уравнения, описывающего турбулентность и этот поток являются considered .In кроме того, Калман предложил e, ₙ= eg или Prra= 1 .С учетом вышеизложенного и допущений поскольку q и m являются константами, выражения буферного слоя (8-32) и (8-33) являются: (8-39) теперь мы используем эти формулы для вычисления перепада температуры буферного слоя .Второй .= — f dy WPr) + » * коэффициент турбулентной вязкости определяется по первой формуле .p du слоистый подслой и толщина буфера Слой незначителен по сравнению с радиусом трубы .
Поэтому в этих слоях напряжение трения и удельный тепловой поток изменяются лишь на очень малых величинах .、 Permanent .In в соответствии с этим мы заменяем mb и qb на Tw и qw> и вводим безразмерную величину⁺ из уравнения, определяющего эти величины, в p du__ _ 1 du + ^ wdy уравнение Калмана скорости буферного слоя v dy + ’ дает du * /dy * = 5/ .Таким образом, получается, что вы выполнили Y *и y «Д/» = — btcₚ4j (l / Pr) + (y * / 5) — l f / l _ 3⁰ / Z%, F (I/ Pr) + (0⁺ / 5) -L•5 Интеграл: h =-b ?СР * СР ды ды + J и / ^ 51n (5Pr + л) .Падение температуры ламинарного подслоя определяется как линейная 5pr уравнение .В » _ ПР а / ₍₍^^=__yᵢ .
Присвоение безразмерной величины y * (y * = 5) происходит в турбулентном слое по аналогии Рейнольдса[уравнение (8-10) ] или Из Интеграла уравнения (8-37), предполагающего qjx = const и Pr, = 1, получаем следующую формулу: btt = ^ yt-p ’■подстановка величины без размерности y дает: границу зоны турбулентности .равное b, расстояние от стены фиксируется на # + = 30 .So если вы используете уравнение Калмана и* = 5 (1-f-log g / ⁺ / 5) и # ⁺= 30, вы получаете: Найти общую разность температур между стенкой трубы и концом зоны турбулентности (осью трубы) : W s и ⁶J безразмерные Равный к передаче тепла: e_ Nu nu RePr-9c (tw-tₛ)^ _______________ _____________________1+ K WP «* {5 (Pr-1) + 5 In [ (5 Pr + 1) / 6]}}это решение заменяет решение (8-12), был выведен Прандт-Лемом и Taylor .It эффективен как для плоских пластин, так и для pipes .
To примените это решение при расчете теплопередачи плоской Сляб, необходимо сделать замену MFF- (cm-STR-179) : ?US z st-NUx—R ^ pF = 1 + J / 772 {5 (Pr-1) 4-5 в Ts5 Pr 4-1) / 6]} ’ гладко При расчете поверхностного коэффициента теплопередачи fₚ/ 2 ~ 0296 (ReJ⁰, 2) в трубе необходимо помнить, что коэффициент теплопередачи обычно рассчитывается из Средней интегральной температуры tB потока .В приведенном выше уравнении, с другой стороны, применяется температура tₛ среды вдоль оси трубы .
Формула для определения напряжения трения на стенке трубы также включает среднюю скорость um .Это не скорость вдоль оси Uₛ трубы, используемой в рассматриваемом уравнении .ₘ ^=ujuₛ и, аналогично ЛТ£) извести замену ’ с£С . / П ^ » / / ^ («Р .196), то вам трубы: ₛₜ ₌ ₌ привирать____________ RedPr 1 + ?/ ₙ/ / 78 {5 (пр-я) 4-5 в [ (5 пр + я) / 6ДЖ} ’ Значение отношения скоростей поля скоростей в турбулентном режиме (его можно найти по формуле (6-32) :rp = 0, 82) .По словам Рейнольдса standards .To определить коэффициент трения f можно, применив соотношения (6-55) или (6-56) .Вы можете построить его с помощью специальной системы координат Кривая .
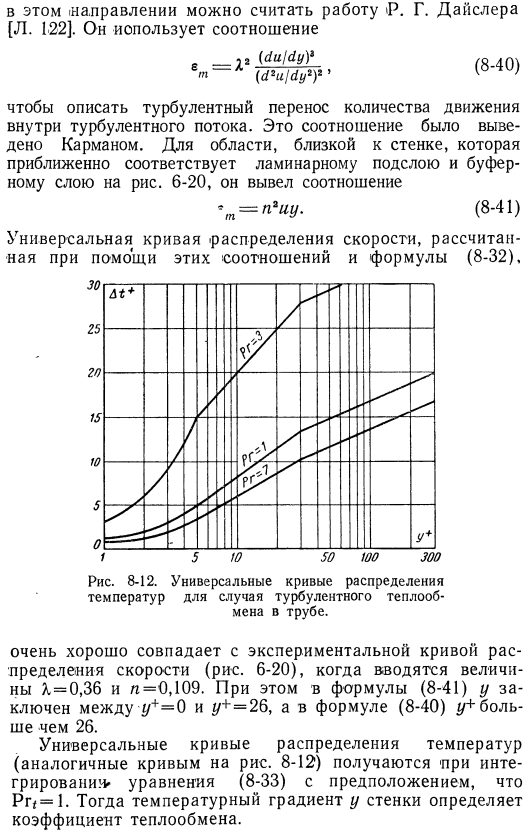
Так как это немного зависит от критерия Рейнольдса, распределение температуры является Аналогия с универсальным распределением скоростей curve .In в Формуле для разности температур в разных слоях есть член с размерами температуры .Дифференциальное деление Температура между любыми точками■температура в пограничном слое и стенке (/- tw) с указанными выше коэффициентами дает безразмерную величину Д/⁺ .Универсальное распределение температуры curve .As на графике рисунка абсцисса будет такой же (#+) .6-20 .На рис .8-12 показаны различные кривые распределения температуры.
Значение ссылки Prantle .Кривая для Pr = 1 идентична универсальной кривой распределения скоростей, когда коэффициенты переноса импульса и тепловой турбулентности равны .Построение кривой распределения температуры по экспериментальным данным описанным способом позволяет проверить точность допущений, сделанных при изложении теоретических расчетов .В этом разделе .Многие исследования изменили и дополнили эти положения, выдвинутые Кальманом .Это обсуждалось в начале этого раздела .Это особенно распространено и успешно — Направление-Р . Г .Дислер . 122 .Он___ (скучно ?(J2u / d / 2) 2 ’ (8-40) используется для описания турбулентного переноса внутреннего импульса .
Турбулентность .Это соотношение было оценено по формуле Pocket .In область, близкая к стенке, примерно соответствует ламинарному вторичному слою и буферному слою на Рис . 1 .6-20 ему Оцените зависимость= (8-41) универсальной кривой распределения скоростей, рассчитанной с использованием этих соотношений и уравнения (8-32), от температуры корпуса Турбулентный теплообмен в трубе .Если ввести значения X = 0 .36 и/ g = 0 .109, то они очень хорошо совпадают с экспериментальной кривой распределения скоростей (рис .6-20) .
Также в Формуле (8-41) y заключен между 2 /⁺= 0 и r /⁺= 26, а y +больше 26 в уравнении (8-40) .Получена универсальная кривая распределения температуры (аналогичная кривой на рис .8-12) при Интеграл уравнения (8-33) в предположении, что Pr = 1*, то градиент температуры стенки определяет теплообмен coefficient .In таким образом, дисслер Теплообмен в трубе в условиях турбулентного течения и течения пограничного слоя воздуха хорошо согласуются с экспериментальными данными data .In эти расчеты, предположил он Число Прандтля и удельная теплоемкость постоянны, а вязкость и теплопроводность изменяются пропорционально абсолютной температуре 0, 68 .
После этого передача тепла и подача будут зависеть Из дополнительной пары, обратной безразмерной температуре, как это сделано на фиг .8-12 .Дишлерс проанализировать не только влияние скорости потока в трубе、 Другие потоки, в том числе близкие к критическим states .As как видно из немецкой литературы, аналогичное исследование турбулентного теплообмена было проведено х .Это сделал Райхард .[Л .123] .Выводы этого раздела должны распространяться на вещества с низким значением критерия Прандтля, например, расплавленные metal .In эти вещества.
Как и в предыдущих расчетах, мы рассматриваем молекулярный обмен импульсом и теплом в турбулентном режиме .Такое распределение называется R . S . Martinelli [L .−124] .Задача 8-1 .Рассчитайте и сравните мощность, необходимую для преодоления перепада давления воздуха, проходящего через воздушный охладитель, чтобы лететь со скоростью 800 км {ч, если в канале охладителя (а) скорость воздуха относительно плоскости уменьшается на 1/10 до поступления воздуха в охладитель, если только (6) скорость уменьшается Понемногу .
Температура воздуха составляет −45 ° С и поднимается на 22°С по мере прохождения через охладитель .Чиллер используется для охлаждения Масло 2, 7 кг (121-65°C в конвекции .Площадь поверхности теплообмена также сравнивается, принимая во внимание, что коэффициент теплопередачи увеличивается пропорционально .Порядка 0 .8 массовой скорости Ри .Используйте приблизительный Pr = 1 .8-2 .Рассчитайте и замените длину теплового начального участка температурного поля и турбулентности через трубу Фактическое поле скорости при постоянной скорости по поперечному сечению трубы .
Рассмотрим, что кривая распределения температуры вблизи стенки аппроксимируется законом 7-го порядка Используйте уравнение (11-14) для описания локального теплового потока через поверхность трубы .Сравните результаты этих расчетов с информацией из раздела 8-2、 Чем фактическое состояние отличается от допущений, сделанных в этом расчете ?8-3 ’ .Вычислите тепловой пограничный слой вдоль верхней пластины Исходя из следующих допущений: течение ламинарное до критического значения критерия Рейнольдса Rec .Затем он быстро становится турбулентным и в критической точке Конвективная толщина турбулентного пограничного слоя равна конвективной толщине ламинарного слоя .
Поток имеет критерий Priidtl равный I .выведите соотношение между средними значениями Сравнение критерия нуссельта с соотношением 271 стр .8-4 .Вычислить локальный коэффициент теплопередачи турбулентного пограничного слоя вдоль плоской пластины、 Предположим, что разность температур между потоком и поверхностью увеличивается линейно с расстоянием от передней кромки .§Использование методов и отношений, описанных в разделе 7 .4 Передача тепла от раздела 8-3 к постепенному изменению в температуре стены .8-5 .Выведите уравнение теплопередачи, вызванной турбулентностью на плоской пластине .
Однако, поскольку пластина не нагревается на расстоянии xo, температура в этой части равна температуре потока, а ниже по потоку от точки xq、 Постоянная температура .Используя закон 7 градусов, опишите кривую распределения температуры и уравнение локального теплового потока (11-14) .Обосновать расчет Термический пограничный слой начинает формироваться при x = x0, и этот пограничный слой превращается в Быстрый пограничный слой .Проинтегрировать уравнение Энергетический пограничный слой .
Сравните результат с выражением на стр . 271 .8-6 .Графическое построение определяемой турбулентности и изменения ламинарного напряжения сдвига Рисунок уравнение 6-20 и перпендикуляр к поверхности в 8-4 раздел .Проанализируйте, насколько фактические условия отличаются от предполагаемых во время строительства Графика .
Смотрите также:
| Движение жидкости в трубе | Анализ явлений теплообмена с применением теории размерности |
| Продольное обтекание плиты | Поперечное омывание труб и пучков труб |

