Поперечная сила и изгибающий момент
При изгибе балки, вызванном действием приложенных к ней внешних моментов, в поперечных сечениях возникают внутренние силовые факторы — изгибающие моменты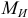 
. Аналогичное явление имеет место в случае простого поперечного изгиба, если горизонтальный брус, лежащий на двух опорах, подвергнуть действию вертикальных нагрузок в продольной плоскости симметрии бруса. При этом наряду с изгибающим моментом в поперечных сечениях возникнет поперечная сила 
.
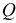Рассмотрим методику определения изгибающего момента 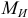и поперечной силы. Пусть балка, лежащая на опорах 
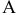и 
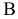(рис. 2.24), нагружена вертикальными силами 
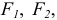распределенной нагрузкой интенсивности 
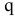и моментами 
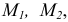действующими в вертикальной плоскости симметрии балки. Опорные реакции 
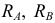в точках 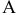и 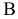можно определить из уравнений равновесия всей балки.
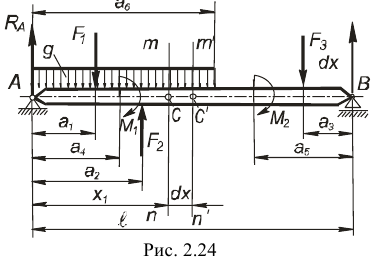
Рассмотрим поперечное сечение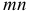 
балки, определяемое абсциссой 
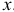. Указанное сечение делит внешние силы и моменты, приложенные к балке, на две взаимно уравновешивающиеся системы, из которых одна действует слева, а другая — справа от данного сечения.
Каждую из этих систем можно привести к центру тяжести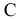 
рассматриваемого сечения. Тогда главный вектор и главный момент относительно центра 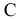сил, действующих слева от сечения, должны быть соответственно равны по модулю и противоположны по направлению главному вектору и главному моменту относительно того же центра сил, действующих справа от этого сечения. Указанные главный вектор 
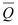и главный момент 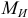являются статическими эквивалентами внутренних сил, возникающих при изгибе в поперечном сечении.
Главный вектор внешних сил, действующих на балку по одну сторону от данного сечения, называется поперечной силой в данном сечении. Если некоторые силы, действующие на балку, не перпендикулярны к ее оси, то поперечной силой называется вертикальная составляющая главного вектора внешних сил, расположенных по одну сторону от данного сечения.
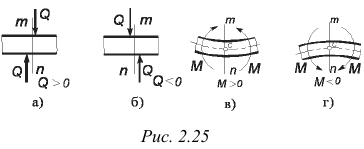
Ограничиваясь случаем параллельных сил, можем поперечную силу (обозначим ее через 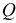) рассматривать как алгебраическую величину, имеющую положительное значение, если для левой части балки она направлена вверх, а для правой — вниз (рис 2.25, а), и отрицательное при противоположном направлении (рис. 2.25, б).
Таким образом, поперечная сила 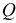в любом поперечном сечении балки численно определяется как алгебраическая сумма сил, расположенных по одну сторону от сечения.
Для сечения 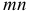(см. рис. 2.24) в соответствии с установленным правилом знаков имеем
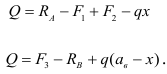
Главный момент внешних сил, действующих на балку по одну сторону от данного сечения, относительно центра тяжести этого сечения, называют изгибающим моментом в данном сечении. Этот момент (обозначим его через 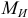) будем рассматривать как алгебраическую величину, имеющую положительное значение, если он действует так, что ось балки изгибается выпуклостью вниз (рис. 2.25, в), и отрицательное в противоположном случае (рис. 2.25, г). Изгибающий момент 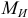в любом сечении балки численно определяется как алгебраическая сумма моментов, действующих на балку внешних сил, расположенных по одну сторону от рассматриваемого сечения, относительно центра тяжести этого сечения. При этом для левой части балки моменты сил считаются положительными, если они направлены по отношению к центру тяжести сечения по часовой стрелке, и отрицательными, если против часовой стрелки; для правой части — наоборот.
Таким образом, для сечения 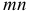(см. рис. 2.24) имеем
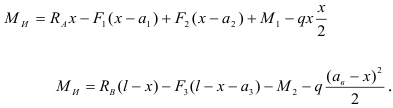
Поперечная сила 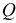и изгибающий момент 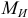в общем случае зависят от положения сечения, т.е. от абсциссы 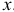. Найдем зависимость между величинам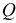и и 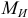, а также 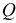и 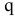. Для этого определим поперечную силу 
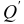и изгибающий момент 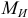в сечении 
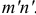смещенном относительно сечения 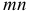на бесконечно малое расстояние 
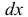(см. рис. 2.24);
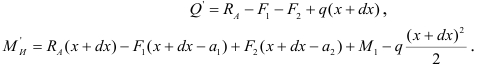
Определим изменения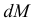 
изгибающего момента и 
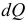— поперечной силы при переходе от сечения 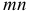к сечению 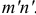. Вычитая соответственно (2.30) из (2.32) и (2.29) из (2.31), имеем
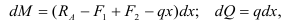
откуда, учитывая выражение (2.29), получаем
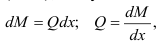
т.е. поперечная сила в данном сечении равна первой производной от изгибающего момента по абсциссе сечения (теорема Д. И. Журавского). Аналогично получим
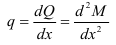
т. е. вторая производная от изгибающего момента по абсциссе сечения равна интенсивности распределенной нагрузки.
Полученные зависимости используют при построении эпюр изгибающих моментов и поперечных сил. Графики зависимости изгибающего момента 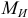и поперечной силы 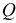от координаты 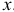сечения называют эпюрами изгибающих моментов и поперечных сил. Эпюры дают наглядное представление о характере изменения изгибающего момента и поперечной силы по длине балки и позволяют устанавливать местонахождение опасных сечений.
Рассмотрим методику построения этих эпюр для простейших случаев нагружения.
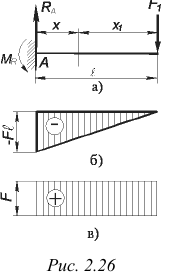
Случай 1. Консольная балка нагружена сосредоточенной силой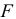 
на конце консоли (рис. 2.26, а).
В месте защемления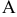 
балки возникает реактивный момент 
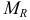и опорная реакция 
.
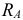Составим уравнения равновесия сил, действующих на балку:
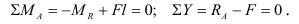
Отсюда
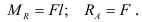
Определим изгибающий момент в сечении, расположенном на рас-стоянии от опоры 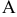. Силы, действующие слева от рассматриваемого сечения, создают момент
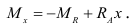
После подстановки значений реактивного момента и опорной реакции приходим к следующему уравнению:
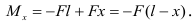
Пр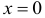и 
и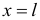 
получаем изгибающий момент соответственно у опоры 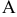и на конце балки:
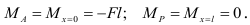
Построим эпюру изгибающих моментов. Для этого выбираем нулевую линию, параллельную оси балки.
Откладывая в некотором масштабе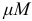 
от этой линии вниз (
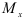< 0) под соответствующими сечениями балки найденные значения 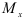, получаем искомую эпюру (рис. 2.26, б). Так как зависимость 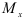от координаты сечения в данном случае является линейной, то эпюра изгибающих моментов представляет собой наклонную прямую. Абсолютная величина изгибающего момента достигает наибольшего значения у закрепленного конца балки.
Рассмотренную задачу можно решить проще, если за начало отсчета координаты сечения принять точку приложения силы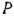 
и определять главный момент сил, находящихся справа от сечения. Обозначая новую координату сечения через 
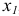имеем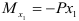 
; на концах балки получаем
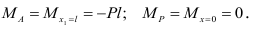
Для определения поперечных сил обратимся к теореме Журавского:
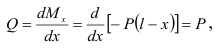
т. е. поперечная сила постоянна по всей длине балки. Эпюра поперечных сил в данном случае представляет собой прямую, параллельную нулевой линии и отстоящую от нее на расстоянии 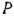(рис. 2.26, в) в масштабе 
.
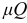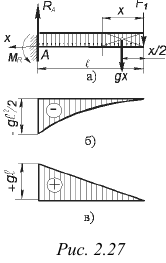
Случай 2. Консольная балка нагружена по всей длине равномерно распределенной нагрузкой с интенсивностью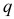 
(рис. 2.27, а).
Реактивный момент в этом случае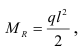 
опорная реакция 
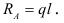. Заменив равномерно распределенную нагрузку, действующую на правую часть балки, сосредоточенной силой, равной 
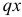и действующей на расстоянии 
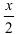от выбранного сечения, имеем
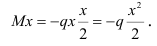
Определим значение изгибающих моментов для характерных точек:
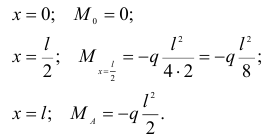
Как видно из уравнения (2.35), эпюра изгибающих моментов в данном случае представляет собой параболу второй степени, обращенную вогнутостью вниз и с вершиной в начале координат (рис. 2.27, б). Эта парабола может быть построена по точкам. Абсолютная величина изгибающего момента имеет наибольшее значение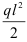 
у защемленного конца балки. На основании теоремы Журавского
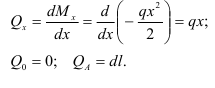
Из уравнения (2.36) следует, что эпюра поперечных сил наклонная прямая (рис. 2.27, в).
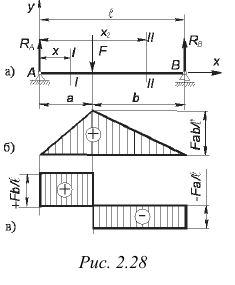
Случай 3. Балка на двух опорах нагружена сосредоточенной силой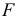 
(рис. 2.28, а).
Составим уравнения равновесия балки:
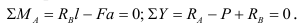
Отсюда
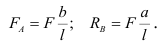
Рассмотрим два сечения, определяемых координатам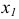и 
и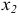 
. Первое сечение расположено между опорой 
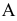и точкой приложения силы 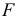, второе — между опорой 
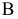и точкой приложения силы .
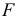Изгибающий момент в сечении I-I, если рассматривать левую часть балки.
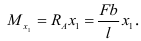
Изгибающий момент в сечении II-II
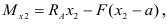
т. е. изгибающий момент на двух участках балки определяется двумя линейными уравнениями, и, следовательно, эпюра изгибающих моментов состоит из двух отрезков прямой (рис. 2.28, б). Величина изгибающих моментов в характерных точках
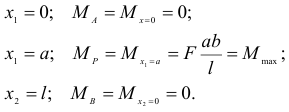
Если сила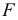 
приложена в середине пролета, т. е. 
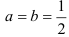то
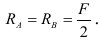
Максимальный изгибающий момент в этом случае
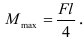
Так как изгибающий момент выражается двумя линейными функциями координаты сечения, то из теоремы Журавского следует, что на каждом из двух участков между опорами и точкой приложения сосредоточенной нагрузки 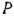поперечная сила остается постоянной.
Действительно, для участка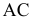 
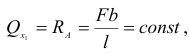
для участка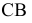 
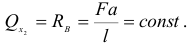
Таким образом, эпюра поперечных сил представляет собой два прямолинейных отрезка, параллельных нулевой линии (рис. 2.28, в). В точке приложения нагрузки 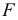поперечная сила меняется скачкообразно.
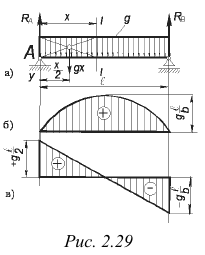
Случай 4. Балка на двух опорах нагружена равномерно распределенной нагрузкой интенсивностью 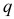(рис. 2.29, а).
Равнодействующая равномерно распределенной нагрузки равна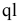 
и приложена в середине пролета балки. Поэтому
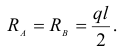
Изгибающий момент в сечении I-I на расстоянии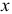 
от левой опоры
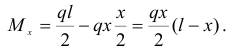
Изгибающий момент в характерных точках
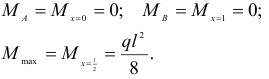
Эпюра изгибающих моментов представляет собой параболу второй степени (рис. 2.29, б).
Величину поперечной силы в сечении I-I определяем как сумму внешних сил, действующих слева от сечения:
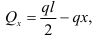
т. е. поперечная сила изменяется по линейному закону. Определим ее величину в характерных точках:
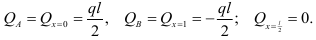
Эпюра поперечных сил представляет собой наклонную прямую, пересекающую нулевую линию в середине пролета балки (рис. 2.29, в).
Эта теория взята со страницы лекций по предмету «прикладная механика»:
Возможно эти страницы вам будут полезны:
