Понятие знакочередующегося ряда. Признак Лейбница

Важный класс числовых рядов образуют знакочередующиеся ряды.

Ряд называется знакочередующимся, если положительные и отрицательные члены ряда следуют друг за другом поочередно. В общем виде знакочередующийся ряд можно записать следующим образом:

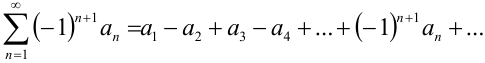, где 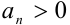для всех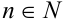

Так, знакочередующимися являются ряды:

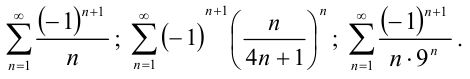
Для заданного знакочередующегося ряда легко можно найти любой его член. Это осуществляется подстановкой в формулу общего члена ряда номера искомого члена.

Пример №34.1.

Выпишите три первых члена знакочередующегося ряда .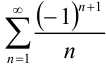

Решение:

Общий член заданного ряда выражается формулой 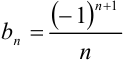. Тогда первый член ряда 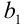найдём подстановкой в эту формулу значения 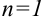, т.е. 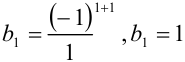. По аналогии найдём второй и третий члены ряда:

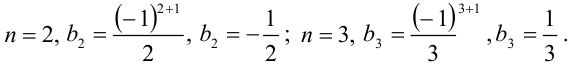
Таким образом, можно записать: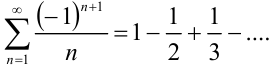

Ответ: 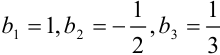или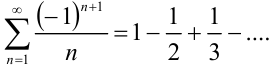

Для знакочередующихся рядов имеет место достаточный признак сходимости, впервые изложенный в 1714 году Г.В. Лейбницем в письме к И. Бернулли. В настоящее время данный признак известен как признак Лейбница. Сформулируем его без доказательства.

Признак Лейбница. Если последовательность абсолютных величин членов знакочередующегося ряда 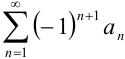монотонно убывает 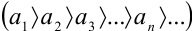, и общий член ряда стремится к нулю 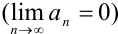, то знакочередующийся ряд сходится.

Доказывать сходимость знакочередующегося ряда 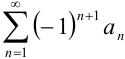по признаку Лейбница удобно с помощью алгоритма:

1. выписать модуль общего члена исходного ряда ;
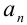2. найти 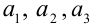и проверить выполнение неравенств: ;
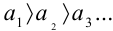3. найти предел общего члена ряда 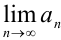и убедиться в том, что он равен нулю.

Пример №34.2.

Исследуйте сходимость знакочередующегося ряда 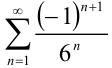с помощью признака Лейбница.

Решение:

Для исследования сходимости знакочередующегося ряда по признаку Лейбница воспользуемся алгоритмом.

1. Выпишем модуль общего члена исходного ряда: .
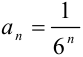2. Найдём 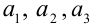: 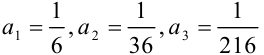. Неравенства 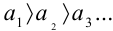справедливы, т.к. 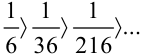(тем самым первое условие признака Лейбница выполняется).
3. Найдём 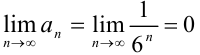(второе условие признака Лейбница выполняется).

Следовательно, по признаку Лейбница знакочередующийся ряд 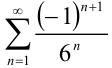сходится.

Ответ: 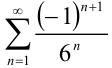сходится.

Ряд, для которого выполняются условия признака Лейбница, называется лейбницевским (или рядом Лейбница). Сумма ряда Лейбница 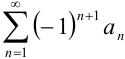положительна и удовлетворяет неравенству: .

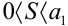Так, ряд 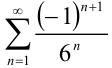, рассмотренный в примере 34.2., по определению является лейбницевским и имеет положительную сумму, не превосходящую .

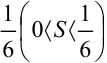Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:

Предмет высшая математика

Другие лекции по высшей математике, возможно вам пригодятся:

Признак Коши (радикальный).

Интегральный признак Коши.

Абсолютная и условная сходимость знакочередующегося ряда.

Свойства абсолютно сходящихся рядов.