Оглавление:


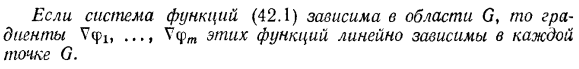

Понятие зависимости функций
Понятие зависимости функций. НОпределение 1.Открыть набор Cc /?Это дает непрерывно дифференцируемую функцию. У1 =ФМ (х), 1 = 1.2,м, х =(Х1,…ЕК, ХL). (42.1) Пространство ю -.1 Если имеется открытый набор И… И дифференцируемая функция φ (Y1,…, ym -), xe C в любой точке Состояние (Ци(х) ft_x(х))= andΦ(ц(х),…. Ци-х(х))= м(х)、 Функция ft вызывается в зависимости от множества O функции FT… Определение 2.Если среди функций системы (42.1) есть функции, зависящие от других функций множества C, то эта система называется зависимой от множества C. Если функция системы (42.1) не зависит от других функций множества C, то эта система называется C-независимой. $ 42.Зависимости функций Восемьдесят шесть. II dU1 II и X / 1 = 1, 2,… t; / = 1, 2,…. н、 (42.2)
Для краткости вместо выражения «зависимая (независимая) функциональная система» можно также просто сказать «зависимая (независимая) функция». Людмила Фирмаль
- В задаче о зависимости функциональной системы (42.1) якобианская матрица этой системы играет фундаментальную роль I-номер строки,/ номер столбца. Теорема 1 (условие, необходимое для функциональной зависимости). предположим, что m> n и функциональная система (42.1) зависят от открытого множества C. Тогда в любой точке этого множества ранги Якобиана (42.2) этой системы меньше m. Proof. As гипотеза, система функций (42.1) зависит от 0.То есть, по крайней мере, 1 из этих функций зависит от других functions. To будьте ясны, предположим, что pm зависит от Ф1.* * * Фт-1* м (х)=φ (ХХ (х),… м-Х(Х), Х (^6、 Где Φ-число аргументов y (m-1)…YM \является непрерывной дифференцируемой функцией. Отсюда Т-1 н. Все y = 1, 2. дю, н _ г dFdu1 ДХ / ^ du1 ДХ.
- Эта формула показывает, что N-я строка Якобиевой матрицы в каждой точке xeC (42.2) является линейной комбинацией оставшихся строк этой матрицы, и поэтому ранг якобиевой матрицы в каждой точке xeC (42.2) меньше m. [] Последствия 1. пусть m-n и система функций (42.1) зависят от O. После этого Якобиан Yn \будет равен нулю во всех точках множества. О. Система 2 (достаточное условие функциональной независимости). если взять m> n и уравнять ранг (42.2) Якобиевой матрицы с m хотя бы 1 точкой в открытом множестве, то система (42.1) будет независима от множества C.
Это число соответствует максимальному минорному порядку этой матрицы, но оно не равно нулю. Людмила Фирмаль
- Система 1 непосредственно вытекает из доказанной теоремы m-N. Система 2 легко доказывается противоречием. Поскольку строки Якобиевой матрицы (42.2) являются координатами градиента функции (42.1), теорему 1 можно перефразировать следующим образом: * ’Напомним, что ранг матрицы-это максимальное число линейно независимых строк.42.2.Достаточные условия для функциональной зависимости Восемьдесят семь Если система функций (42.1) зависит от области C, то градиент Uf этих функций! Upt линейно зависит от каждой точки O. еобходимое условие зависимости функций.
Смотрите также:
Решение задач по математическому анализу

