Величины, которые полностью определяются своими численным значением, называются скалярными. Примерами скалярных величин являются: площадь (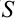
), длина (
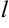), объем (
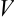), температура (
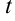), работа (
), масса (
).
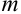Другие величины, например, сила (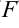
), скорость (
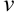), ускорение (
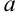), определяются не только своим числовым значением, но и направлением. Такие величины называют векторными. Векторная величина геометрически изображается с помощью вектора.
Вектор — это направленный отрезок, т.е. отрезок, имеющий определенную длину и определенное направление.
Если — начало вектора, а 
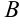— его конец, то вектор обозначается символом 
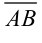или 
.
Вектор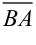 
(имеет начало в точке 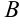, а конец в точке ) называется противоположным вектору 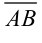. Вектор, противоположный вектору , обозначается 
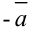(рис. 5.1).
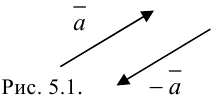
Длиной или модулем вектора 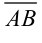называется длина отрезка 
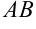и обозначается 
.
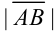Вектор, длина которого равна нулю, называется нулевым вектором и обозначается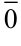 
. Нулевой вектор не имеет направления.
Вектор, длина которого равна единице, называется единичным и обозначается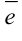 
.
Векторы и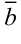 
называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают 
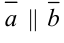(рис. 5.2).
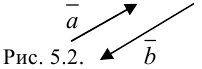
Коллинеарные векторы могут быть одинаково (рис. 5.3.) или противоположно (рис. 5.2.) направлены.
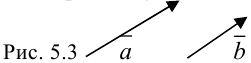
Нулевой вектор считается коллинеарным любому вектору.
Два вектора и 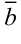называются равными (
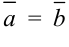), если они одинаково направлены и имеют одинаковые длины.
Все равные между собой направленные отрезки называют свободным вектором. Свободный вектор может быть отложен от любой точки пространства. В дальнейшем мы будем оперировать понятием свободного вектора.
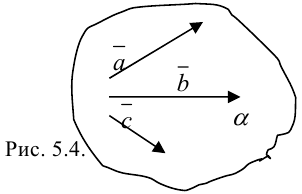
Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях (рис. 5.4.).
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
