Для нахождения ранга матрицы ее нужно привести к ступенчатому виду: под первым ненулевым элементом каждой ее строки стоят нули в нижних строках:
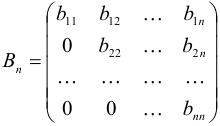
Теорема. Ранг ступенчатой матрицы равен числу ее ненулевых строк.
Ранг матрицы обозначается 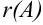 .
.
Приведение матрицы к ступенчатому виду осуществляется с помощью элементарных преобразований:
- умножение всех элементов строки или столбца матрицы на число, отличное от нуля;
- замена строк столбцами и наоборот;
- перестановка местами параллельных рядов;
- вычеркивание нулевого ряда;
- прибавление к элементам некоторого ряда соответствующих элементов параллельного ряда, умноженных на любое действительное число.
Если одна матрица получается из другой с помощью элементарных преобразований, то такие матрицы называются эквивалентными и обозначаются 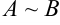 .
.
Для упрощения вычислений на первое место лучше ставить ту строку, в которой первый элемент равен 1.
Пример №3.3.
Найдите ранг матрицы 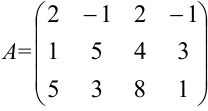 .
.
Решение:
Приведем матрицу к ступенчатому виду с помощью элементарных преобразований.
Поменяем местами первую и вторую строки для того, чтобы первый элемент первой строки был равен 1:
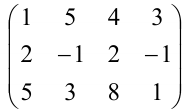
Первую строку больше преобразовывать не будем.
Для того, чтобы первый элемент второй строки был равен нулю, прибавим ко второй строке первую, умноженную на (-2):
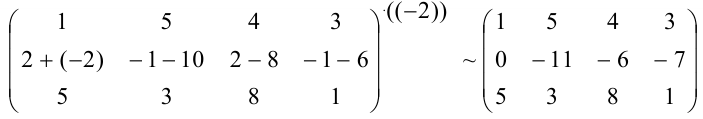
Для того, чтобы первый элемент третьей строки был равен нулю, прибавим к третьей строке первую, умноженную на (-5):
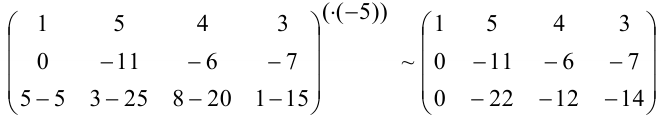
Для того, чтобы матрица имела ступенчатый вид, необходимо, чтобы второй элемент третьей строки был равен 0. Прибавим к третьей строке вторую, умноженную на (-2):
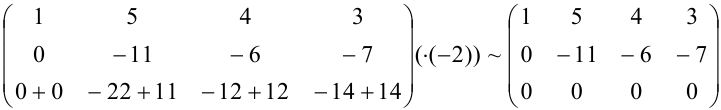
Вычеркнем нулевую строку. В результате элементарных преобразований получили матрицу: 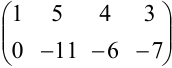
Число ненулевых строк в полученной матрице равно двум, следовательно, ее ранг равен 2, т.е. 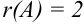 .
.
Ответ: 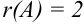 .
.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Понятие обратной матрицы. |
| Алгоритм нахождения обратной матрицы. |
| Понятие решения системы линейных уравнений. |
| Правило Крамера решения системы линейных уравнений с неизвестными. |

