Понятие производной является одним из основных математических понятий. Производная широко используется при решении целого ряда задач математики, физики, других наук, в особенности при изучении скорости различных процессов.
Пусть функция 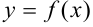 определена на некотором интервале
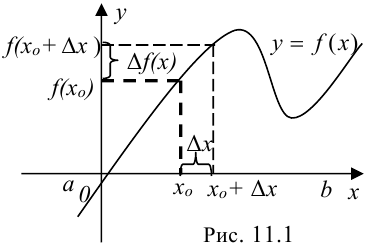
определена на некотором интервале 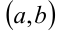 . Проделаем следующие операции (рис. 11.1):
. Проделаем следующие операции (рис. 11.1):
- аргументу
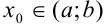 дадим приращение
дадим приращение 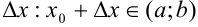 ;
; - найдем соответствующее приращение функции:
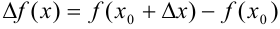 ;
; - составим отношение приращения функции к приращению аргумента
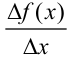 ;
; - найдем предел этого отношения при
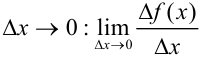 .
.
Если этот предел существует, то его называют производной функции 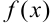 обозначают одним из символов:
обозначают одним из символов: 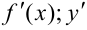 .
.
Производной функции 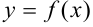 в точке
в точке  называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
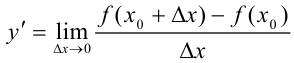 или
или 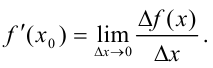
Производная функция 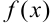 есть некоторая функция
есть некоторая функция 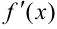 , производная из данной функции.
, производная из данной функции.
Функция 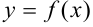 , имеющая производную в каждой точке интервала
, имеющая производную в каждой точке интервала 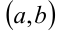 , называется дифференцируемой на этом интервале; операция нахождения производной функции называется дифференцированием.
, называется дифференцируемой на этом интервале; операция нахождения производной функции называется дифференцированием.
Значение производной функции 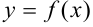 в точке
в точке 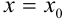 обозначается одним из символов:
обозначается одним из символов: 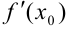 или
или 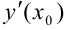 .
.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Непрерывность элементарных и сложных функций. |
| Точки разрыва, их классификация. |
| Нахождение производных основных элементарных функций. |
| Правила дифференцирования функций. |
