Оглавление:


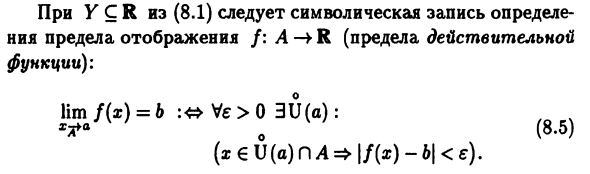

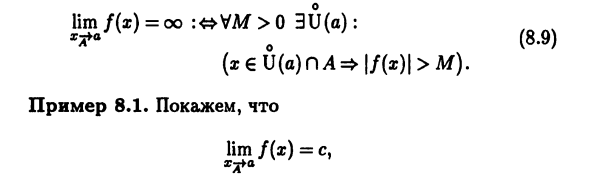







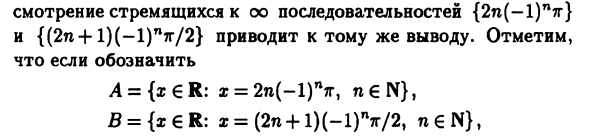




Понятие предела отображения
- Пусть X а-будет заданным метрическим пространством Каждый с метриками PUD и ASA «- Подмножество X с той же метрикой p, € X Конечная точка. Мы, В определении 5.9 оба эти ограничения A могут принадлежать Он никогда не принадлежит подмножеству А. о Проколотая окрестность U (a) = U (a) \ {a} в определенной точке. Карта определения домена // A-> Y Набор А включен. Эта карта для очков Это не может быть определено. Определение 8.1. 6 € Y очков называется лимит A вдоль множества A карты f \ A- * Y и Напишите 6 = lim f (x) или f (x) —► 6, если x-ga,
Какой бы ни была окрестность V (6) точки b, поскольку A имеет проколотую окрестность U (a) точки a, образ о Произвольная точка x∈U (o) АA принадлежит V (6), т. Е. 6 = lim f (x): <* VV (6) CK 3U (a): / (U (a) nA) cV (6). (8.1) При выполнении (8.1) функция f (x) Если x переместится в точку A в множестве A, он будет равен b. Определение 8.1 очень общее. По словам X, Y, AC X и какой набор Покажите, что Ху может получить разные экземпляры этого Определение. Следовательно, в (8.1) любое Электронная окрестность точки 6 € Y окрестности V (6) V (6, e) = {y € Y:%, k) <£}, (8,2) И проколотая окрестность точек € X-та панк ^ -Соседство U (o, S) = {x e X: 0
Запомните любую окрестность точки (см. 5.2) Электронная окрестность этой точки включена и все электронные окрестности Район. Людмила Фирмаль
d (f (x), b) Ve> 0 3U (a): {x £ V (a) nA => \ f (x) -b \ 0 DEF): , (8-6) Если Y — R, вы можете говорить о бесконечных пределах Отображение, когда точка 6 является одной из бесконечных точек (+ Oo или -co) расширенная числовая строка R или Ассоциация (совместная). В этом случае каждый район Формат этих точек при выборе любого М> 0 имеет вид V (+ oo) = {y € Y: y> M} = (M, + co), V (-co) = {yeY: y <-M} = (-oo, -M), V (oo) = {y 6 Y: M> M} = (-co, -M) U (M, + co). Тогда из (8.1) следуют три, которые очень похожи друг на друга. Символическая запись для определения бесконечного предела Особенности: lim fix) = +00: <* VM> 0 3U (o): «» (8.7) (Xe \ J (a) nA => f (x)> M), lim f (x) = -co: <* VM> 0 3U (a): L (8.8) lim / (x) = co: <* VM> 0 3U (a):, v «V; V; (8,9) (X6U {a) DA => \ f (x) > M). Пример 8.1. Покажи это lim f (x) = c, xtfa
Возьмите 1 на карте / установите точку, То же значение с. На самом деле, каким бы ни был район о Поскольку x∈A, V (c) точки c, y∈U (a) A A / (x) = c о / (U (o) nA) = c∈V (c), что соответствует определению 8.1. Пожалуйста, проверьте lim / (x) = a, Если карты / идентичны, то есть / (x) = x Al € A. B о В этом случае для любой окрестности V (a) U (a) = = V (a) \ {a} Идентификационная карта для получения = U (a) nA = (V (a) \ {a}) OAcV (a), Соответствует (8.1). В частности, А = К и А Соответствует расширенной числовой линии бесконечной точке + оо. f (x) -> + oo как x- \ + oo. Конечно, Произвольный M> 0 как проколотая окрестность Для бесконечной точки +00 достаточно выбрать множество U (+ oo) =. = {x € R: x> M} f (x)> получить и удовлетворить M
- Состояние (8,7). # Определение 8.1 белый X = Y = R и подмножество A = = {I 6 R: x> a}, правостороннее понятие Пределы вещественных функций вещественных переменных 7.2 Точка, обозначенная lim fix a). Когда X = Y = R И если A = {x € R: x N * d (yn, b) Y имеет точку Когда х подходит к А, 6 евро Y Отображение / под, до если и если если очков Изображение последовательности точек от А до А Последовательность баллов от Y до 6 Это 6 = lim / () < V {sn} (lim p (xn, a) = 0 = »lim <* (/ (*„), 6) = oY <Предположим, пункт 6 € Y удовлетворен Определение ограничения отображения 8.1, а {xn} является необязательным
Далее согласно (8.1) сосед V (6) C Y о Точка 6, проколотая окрестность U (a) СX существует о k o, f (U (a) OA) C V (6) и т. д. По определению 8.2 о U (o) АA должен начинаться с некоторого числа N +1 Все точки {xn}) последовательности, вероятно, будут a, т.е. Сила (8.10) N: xn ) (a) C) A Vn> N. Тогда все точки с одинаковым номером f (xn) € Y Последовательность {/ (xn)} находится в V (6) Определение 8.2 означает, что эта последовательность имеет тенденцию быть b. Чтобы доказать достаточность условий теоремы, Для любой последовательности {xn} Последовательность точек f (xn) из точек xn из A {f (xn)} Y имеет тенденцию быть б. Для lim f (x) Φ6 это х-фи * Матрица чисел e> 0 для любого выбора 8> 0 Существует точка x∈A, которая удовлетворяет условию p (x, a) <S
Последовательность, в которой точка xn в A стремится указать a € X Людмила Фирмаль
И д (е (х), б) ^ е. Если сколь угодно мало 6> 0, Указывает положительное целое число N такое, что 1 / N <6. Из всех чисел n> N есть хотя бы одна точка из D, Это p (xn, o) <1 / n <1 / Λ <8 d (f (xn), b) ^ e. Следовательно, последовательность {nA}, Состоит из таких точек xn € A, благодаря (8.11) a, {f {xn)} не стремится к 6, и это противоречит Начальное предположение. Полученное противоречие Докажите, что условия теоремы являются достаточными. ► Эта теорема позволяет сформулировать определения.
Эквивалентен определению 8.1. Определение 8.3. Точка b € Y называется пределом Карта A: A-> в вдоль множества A При отображении трендового изображения / Последовательность точек из A является последовательностью точек из U тренд 6. Символический формат записи этого определения Теорема 8.1 согласна. Пример 8.2. Пусть X = R, A = R, a = + oo и в Карта /: R — ►R f (x) = cos a; Va; G R. Покажем это lim fix) = lim cos a: xtfa ar-f + oo Не существует Получить последовательность {xn} = {2n7r} + Стремление к oO. Тогда cosxn = cos2n7r = 1 и сила (6.9) lim {cos xn} = 1 {xn} = {(2n + 1) 7r / 2}, который также стремится к + oo и его изображению
Сходится к нулю. Это противоречит определению 8.3 ограничений Здесь нет картографирования, то есть вышеуказанного ограничения. Рассмотрим тренды последовательности {2n (-1) n7g} И {(2n4-1) (-1) ptg / 2} такой же вывод. ОБРАТИТЕ ВНИМАНИЕ Если мы покажем eR: i = 2n (-1) ptg, n € Запись действительна limcosx = l и Iimcos2 = 0. Сравнение между определениями 8.1 и 5.13 Следующая теорема доказана. Теорема 8.2. Карта /: X- + Y непрерывно Предел Отображение, когда x перемещается в точку A в множестве X Это соответствует значению f (a). время Рила / () = / (<). (8,12) <4. Продолжая отображение / с ∈X. Согласно определению непрерывного отображения 5.13
Точка 6 = f (a) € не существует окрестности V (6) из V / (U (a)) C V (6), такая окрестность U (a) из ∈A, что a о Следовательно, существует проколотая окрестность U (a) точки о такой, что f (U (a)) ⊂V (6). Согласно определению 8.1 это Это означает, что (8.12) выполнено. Обратно, держите (8.12). Тогда в силу Определения 8.1 для любой окрестности V (6) точки b = f (a) cy о Существует проколотая окрестность U (а), как Ах ах / (U (o)) C V (6). Рассмотрим окрестность U (a) = U (a) U {o}. / (A) € V (6) и выше, в зависимости от свойств карты Установить (см. 2.1), » / (U (a)) = / (U (a)) u / (a) cV (6) u6 = V (6), Другими словами, 5.13 является непрерывным в то время по карте / определению Ох. ►
Вы можете сформулировать определения, используя теорему 8.2. Эквивалентен определению 5.13. Определение 8.4. Карта /: называется X- \ Y Если (8.12) выполнено, то оно непрерывно с a∈X. Учитывая теорему 8.1 и 8.2, получим Заявление. Заявление 8.1. Непрерывность отображения /: X- + Y предельная точка € X необходима и достаточна, Отображаемое изображение / Серия очков от X была серией очков Сходимость от Y к точке / (а).
Смотрите также:
| Два замечательных предела | Некоторые свойства предела отображения |
| Экспонента, натуральные логарифмы и гиперболические функции | Пределы действительных функций |

