Пусть функция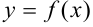 
определена в некоторой окрестности точки 
, быть может, за исключением самой точки .
Число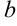 
называется пределом функции 
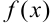при 
, стремящемся к (или в точке ), если для любого наперед заданного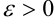 
существует такое 
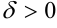, что для всех , удовлетворяющих условиям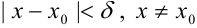 
, имеет место неравенство: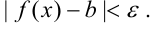 
Если 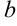есть предел функци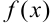и при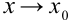 
то пишут: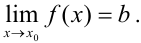 
Это определение предела функции называют определением предела по-Коши (или определением на языке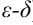 
).
Приведем геометрическую иллюстрацию понятия предела функции в точке (рис. 9.1). Рассмотрим функцию .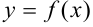
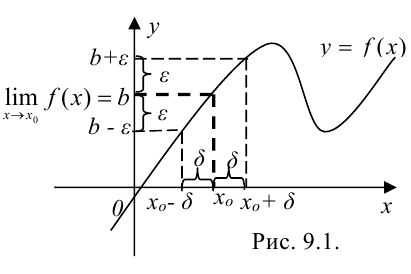
Предел функции 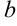ищется по оси 
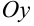. Значение 
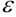выбирают близкое к нулю, это точность, с которой вычисляется данный предел. Чем меньше 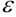, тем выше точность. Для любого 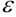можно подобрать такое число 
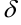, что если выбирать из промежутка 
, то соответствующие значения 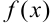будут принадлежать промежутку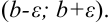 
Другими словами, число 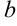является пределом функци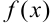и при 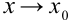, если для всех , близких к и отличных от , соответствующие значения функции мало чем отличаются от числа .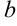
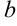Отметим, что при нахождении предела значение функции в точке может быть равно , может отличаться от 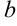, может не существовать.
Рассмотрим следующие примеры:
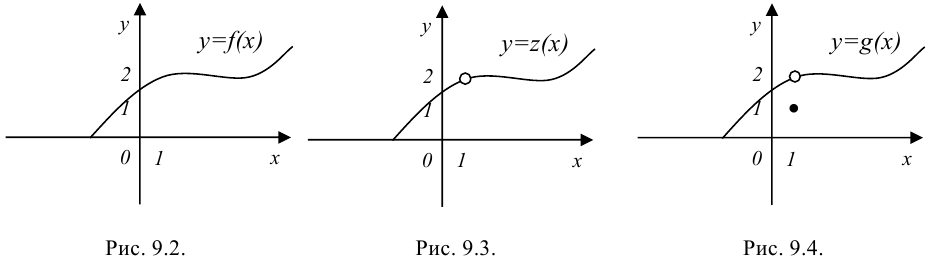
На рис. 9.2 функция определена в точке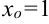 
, причем 
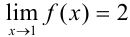(т.к. для всех , близких к 1, соответствующие значения функции близки к 2).
На рис. 9.3 функция не определена в точке 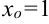, но её предел в этой точке существует, причем 
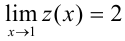. Это связано с тем, что при нахождении предела выбирают значения , близкие к , но отличные от .
На рис. 9.4 функция определена в точке 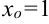, но ее значение в точке не совпадает со значением предела: 
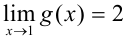, a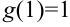 
.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Бесконечно малые и бесконечно большие последовательности. |
| Признак сходимости монотонной последовательности. Число e. |
| Односторонние пределы. |
| Основные теоремы о пределах функции. |
