Понятие плоского движения тела
Плоским или плоскопараллельным называется такое движение твердого тела, при котором все точки тела движутся в плоскостях, параллельных некоторой неподвижной плоскости.
Частным случаем такого движения является уже изученное нами вращение твердого тела вокруг неподвижной оси. При вращательном движении, как мы знаем, все точки тела движутся в плоскостях, перпендикулярных к оси вращения, и следовательно, любая из этих плоскостей может быть принята за неподвижную, параллельно которой движутся все точки тела.
В частности, плоское движение тела может быть одновременно и поступательным движением. Однако поступательное движение нельзя, вообще говоря, рассматривать как частный случай плоского движения. Не всякое поступательное движение тела есть плоское движение, так же как и не всякое плоское движение тела есть поступательное движение.
Представим себе какую-нибудь призму, основание которой любым образом перемещается по неподвижной плоскости 
(рис. 140). При таком движении призмы все ее точки будут, очевидно, перемещаться в плоскостях, параллельных неподвижной плоскости , и потому данное движение призмы будет плоским.
Если при переходе призмы из положения I в положение II, показанных на рис. 140, любая прямая, неразрывно с ней связанная, оставалась во все время движения призмы параллельной своему начальному положению, то движение призмы было плоским и поступательным. При переходе же призмы из положения II
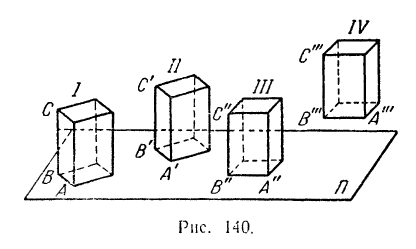
в положение III. как это видно из того же рисунка, уже не всякая прямая, связанная с призмой (как, например, прямая 
), остается параллельной своему начальному положению, и движение призмы за соответствующий промежуток времени уже не будет поступательным, хотя по-прежнему остается плоским. При переходе призмы из положения III в положение IV (рис. 140) основания и боковые грани призмы смещаются в другие плоскости, и движение призмы уже не будет плоским, хотя оно могло быть и поступательным, если во все время данного перемещения любая прямая, неразрывно связанная с призмой, оставалась параллельной своему начальному положению.
Плоское движение имеет огромное распространение в технике. Подавляющее большинство встречающихся на практике механизмов являются плоскими, т. е. представляют собой сочленение твердых тел, совершающих плоское движение.
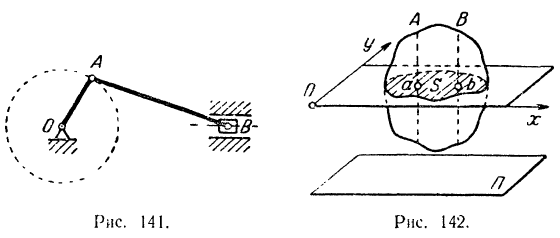
Таково, например, движение всех звеньев кривошипно-шатуниого механизма (рис. 141), состоящего из кривошипа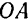 
, ползуна 
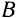и шарнирно соединенного с ними шатуна 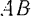. Все точки каждого из этих звеньев движутся параллельно некоторой неподвижной плоскости (плоскости чертежа на рис. 141). Плоское движение кривошипа будет являться вместе с тем и вращательным движением вокруг неподвижной оси 
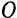. Плоское движение ползуна будет одновременно и поступательным движением вдоль неподвижных направляющих. Плоское же движение шатуна не будет ни вращательным (так как шатун не имеет неподвижных точек), ни
поступательным (nак как прямая 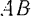не остается при движении шатуна параллельной своему начальному положению) .
Плоское движение совершают: колесо, катящееся по прямолинейному рельсу, механизм спарника и кулисный механизм, рассмотренные в задачах 47 и 48, и многие другие.
Выясним теперь, как можно упростить изучение этого весьма важного вида движения твердого тела. Пусть тело движется параллельно некоторой неподвижной плоскости 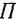(рис. 142). Если мы пересечем данное тело плоскостью 
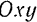, параллельной неподвижной плоскости 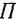, то в сечении получится какая-то плоская фигура 
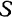. Эта фигура будет перемещаться при движении тела, оставаясь все время в той же плоскости 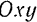. Очевидно, что при плоском движении тела все его точки, лежащие на перпендикуляре 
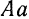к плоскости фигуры 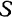, движутся совершенно одинаково, так же как и точка 
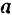этой фигуры. Все точки тела, лежащие на перпендикуляре 
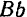к плоскости фигуры 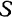, движутся так же, как и точка 
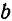этой фигуры, и т. д.
Отсюда следует, что для определения плоского движения тела достаточно знать движение плоской фигуры 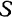(полученной сечением тела какой-либо плоскостью 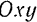, параллельной данной неподвижной плоскости) в ее плоскости.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
