Оглавление:
Каждой квадратной матрице можно поставить в соответствие некоторое число 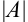 или
или 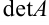 , называемое её определителем, следующим образом:
, называемое её определителем, следующим образом:
- Если дана квадратная матрица первого порядка
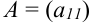 , тогда
, тогда 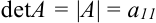 .
.
Пример №2.1.
Найдите определитель матрицы 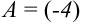
Решение:
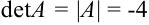 .
.
2. Если дана квадратная матрица второго порядка, то
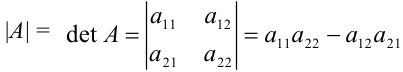
Вычисление определителя второго порядка легко проиллюстрировать схемой:
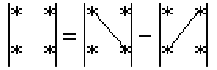
Пример №2.2.
Найдите определитель матрицы 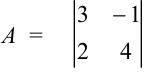
Решение:
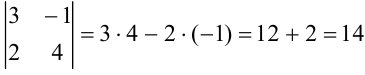
Ответ: 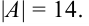
3. Определитель матрицы  третьего порядка вычисляется по правилу треугольников (Сарруса)
третьего порядка вычисляется по правилу треугольников (Сарруса)

Пример №2.3.
Найдите определитель матрицы 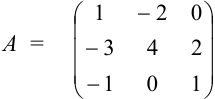
Решение:
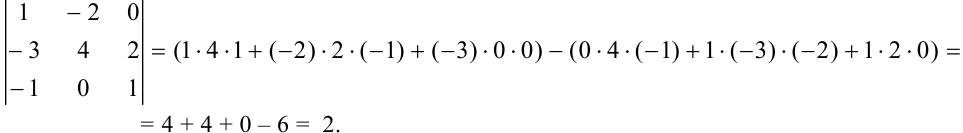
Ответ: 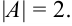
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Равенство матриц. |
| Операции над матрицами. |
| Свойства определителей. |
| Миноры и алгебраические дополнения элементов определителя. |

