Введем сперва понятие однородной функции: функция 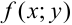 называется однородной функцией
называется однородной функцией 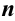 -го порядка, если при умножении каждого ее аргумента на произвольный множитель вся функция умножится на
-го порядка, если при умножении каждого ее аргумента на произвольный множитель вся функция умножится на 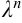 , т.е.
, т.е. 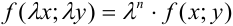 .
.
Пример №39.1.
Доказать, что функции 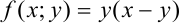 и
и 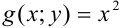 — однородные функции второго порядка.
— однородные функции второго порядка.
Решение:
Рассмотрим функцию 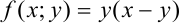 . Подставим в нее вместо
. Подставим в нее вместо 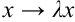 , а вместо
, а вместо 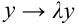 :
:
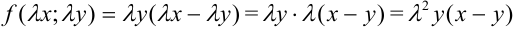 . Получили, что
. Получили, что 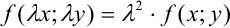 , следовательно, по определению
, следовательно, по определению 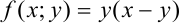 — однородная функция второго порядка.
— однородная функция второго порядка.
Рассмотрим функцию 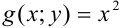 . Аналогично подставив в нее вместо
. Аналогично подставив в нее вместо 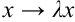 , а вместо
, а вместо 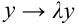 , получим:
, получим: 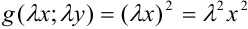 . То есть
. То есть 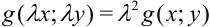 , откуда по определению
, откуда по определению 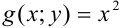 — однородная функция второго порядка.
— однородная функция второго порядка.
Дифференциальное уравнение вида 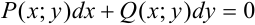 , где
, где 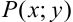 и
и 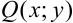 — однородные функции одинакового порядка, будем называть однородным.
— однородные функции одинакового порядка, будем называть однородным.
Так, дифференциальное уравнение 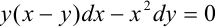 будет являться однородным в силу того, что обе функции при
будет являться однородным в силу того, что обе функции при 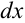 и
и 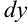 — однородные второго порядка (см. пример 39.1).
— однородные второго порядка (см. пример 39.1).
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:

