Квадратная матрица 
называется вырожденной, если ее определитель равен нулю, и невырожденной, если ее определитель отличен от нуля.
Матрица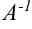 
называется обратной для матрицы , если выполняется условие
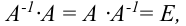
где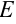 
— единичная матрица того же порядка, что и матрица .
Если обратная матрица 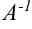существует, то матрица называется обратимой. Нахождение обратной матрицы имеет большое значение при решении систем линейных уравнений и в вычислительных методах линейного программирования.
Встает вопрос: для каждой ли матрицы существует обратная? Примем без доказательства следующую теорему:
Теорема. Всякая невырожденная квадратная матрица имеет обратную.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Теорема о разложении определителя по элементам строки или столбца. |
| Расчет определителей в электронных таблицах Microsoft Excel. |
| Алгоритм нахождения обратной матрицы. |
| Понятие ранга матрицы. |
