Обратные функции, свойства, графики

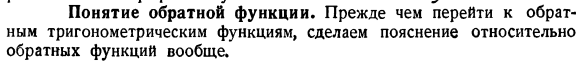
Понятие обратной функции

Понятие обратной функции. Прежде чем перейти к обратной тригонометрической функции, мы обсудим общие обратные функции. Предположим, что функция^ = /(x) задана в области 5C, а Y-это набор всех значений, которые эта функция принимает при изменении x в области 5C. In в нашей практике и так, и Б » обычно представляют собой пробелы. Выберите значение y = yo из области 3^. в области 5C нам нужно найти значение x = xyY, где функция принимает значение Y0>точно. / С * О)= вы Там может быть несколько подобных значений x6.Таким образом, каждое значение y из 3 ^связано с более чем 1 значением x. It определяет площадь и однозначную или многозначную функцию x = H (y). Это называется обратной функцией функции y = f (x).Давайте рассмотрим несколько примеров. 1. пусть y = ax(a> 1).

В этом случае мы видим, что обратная функция уникальна. Людмила Фирмаль

• Где X изменяется с интервалом 5С =(оо, {оо). значение y заполняет промежуток Y =(0,+ oo), и каждый из этих интервалов, как известно[12], соответствует X с определенным x = \ o% ay. In 2.И наоборот, если функция y = xh>, будет ли x изменяться на интервале 3? =(—Oo,+ oo), обратная функция будет иметь 2 значения. Для каждого значения y из интервала 3 ^ = [0, | oo) существует от 3 до 2 значений x =±Yy. Вместо этой 2-значной функции обычно 2 однозначные функции рассматриваются отдельно* = / Yy и x = Y-y («ветвь» 2-значной функции).Вы также можете думать о функции Y = x \наоборот индивидуально, в предположении, что переменные области x разделены интервалами[0, -| -°°) или интервалами (—oo, 0] соответственно.

• Заметим, что по графику функции y = f(x) можно легко вычислить, является ли обратная функция функции x = $(y) уникальной. Первый случай показан, когда линия, параллельная оси xb, пересекает этот график только с одной точкой. И наоборот, если некоторые из этих линий пересекают график в нескольких точках, обратная функция является multi-valued. In в этом случае легко разделить интервал изменения x на части, согласно schedule. So каждая часть уже имеет четкую «ветвь» этой функции. Например, если вы посмотрите на параболу, рис. 14 Если функция x = $(y) является обратной функции y = f (x), то, очевидно, график обеих функций будет совпадать. Однако можно запросить, чтобы аргумент обратной функции указывался символом xY. То есть вместо функции x = $(y) рассмотрим y = k (x).

Если вы хотите, чтобы (новая) ось x была горизонтальной, как обычно, а (новая) ось y была вертикальной, вам нужно переместить эти оси на другую ось. Людмила Фирмаль

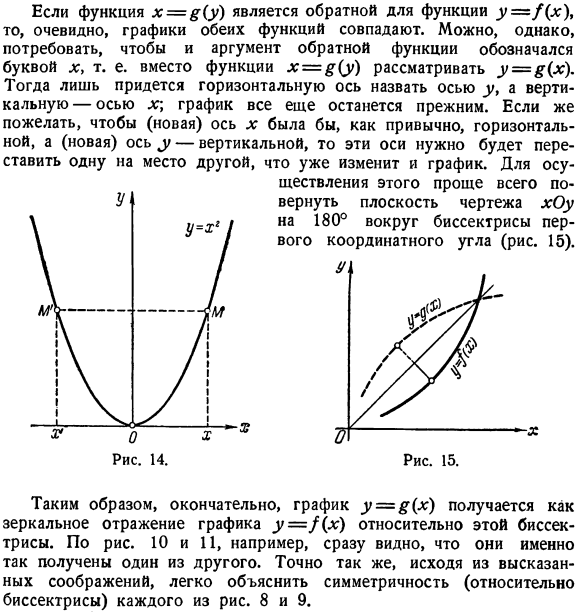
• Тогда просто позвоните по горизонтальной оси у9 оси и вертикальной оси Х \оси и график остается прежним. Это изменит расписание. Для пчел Для этого проще всего повернуть плоскость чертежа xOy на 180°вокруг биссектрисы первого координатного угла (рис.15). Таким образом, в конечном итоге граф y = $(x) берется как зеркальное отражение графа y = /(x) относительно этой биссектрисы. Например, если вы посмотрите на рисунки 10 и 11, то сразу увидите, что они получены таким образом друг от друга. Аналогичным образом, исходя из вышеупомянутых соображений, легко объяснить симметрию (по отношению к биссектрисам) каждой из фигур 2 и 3. 8 и 9.

Смотрите также:

Решение задач по математическому анализу

Функции натурального аргумента.	Обратные тригонометрические функции.
Элементарные функции.	Суперпозиция функций. Заключительные замечания.