Оглавление:




Понятие о потере устойчивости при напряжениях, превышающих предел пропорциональности
- Понятие потери устойчивости при напряжении за пределами пропорционального предела Вывод формулы Эйлера основан на применении дифференциальных уравнений для упругих линий. Таким образом, эта формула может быть использована, если закон крюка справедлив, то есть критическое напряжение (напряжение сжатия, соответствующее критической силе) не превышает предела пропорциональности: 0kr= — ^E — O PC. (19.29)на самом деле дифференциальное уравнение (19.3), предполагающее
справедливость закона крюка, не подходит, если линейная форма стержня стабильна и напряжение превышает предел пропорциональности. Выведена формула для критического напряжения ОКР. По формулам (19.29) и (19.20)) (19.30) 509 где i2=^min== — p-наименьший квадрат главного радиуса инерции стержня; F = re? — Общая площадь поперечного сечения стержня. Можно ввести безразмерное значение Л=4-,(19.31)
Вызванная гибкость штанги, мы в конце концов получаем «_i2£С Р — ^2» (19.32) То есть, Людмила Фирмаль
критическое напряжение стержня зависит только от упругих свойств материала (модуля упругости Е) и гибкости стержня (а). Функциональная зависимость(19.32) является модификацией выражения Эйлера. В системе координат OCR-a эта зависимость может быть выражена гиперболической кривой, называемой гиперболической кривой Эйлера. В качестве примера приведем такой график(рис. 507) для стальных стержней марки СТЗ, модуль упругости е=2,1*106кгф/см2, предел текучести-2400кгф/СМА,
и пропорциональность о, предел текучести 1ТС=2000кгф / см2. График показывает, что при увеличении гибкости стержня, при увеличении критического напряжения bcrcg£yy критическое напряжение стремится к нулю и наоборот. Приближение гибкости стержня стремится к бесконечности. Однако, согласно формуле из условия применимости уравнения Эйлера (19.29) (19.32), мы имеем °С Р — «» Р-°ПК» И так оно и есть., (19.33) 5г2£ Н С В К $ = 2400 блч=2000 Эпплед| / Тогда уравнение Эйлера, гибкость стержня, нижний предел Апреда,
- который зависит только от свойств материала, то есть в этом случае он становится непригодным ВApred-В3 142 •2 020,10 • 10Е То же самое можно получить графически. Если вертикальная ось (TKR) откладывает значение пропорционального предела (sgpc= — 2000kgf / cm2) и рисует прямую линию, параллельную абсциссе от результирующей точки E, то гипербола на пересечении с Эйлером дает точку L1, а на левой стороне точки M гипербола Эйлера обозначается ломаной линией. Величина напряжения больше
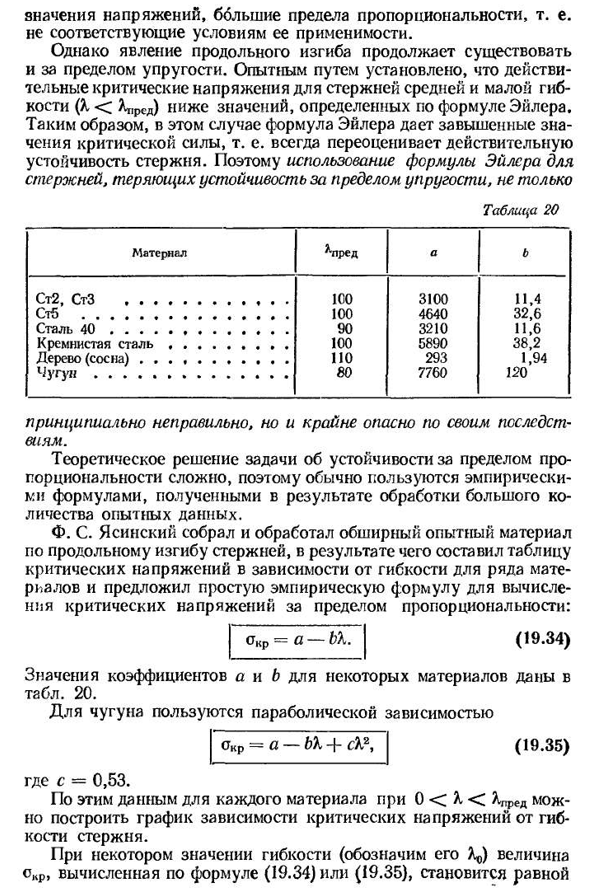
предела пропорциональности 510, то есть не соответствует условиям его применимости. Однако явление продольного изгиба продолжает существовать за пределами предела упругости. Эмпирически установлено, что фактическое критическое напряжение стержня средней и малой гибкости (XLcred) ниже значения, определяемого уравнением Эйлера, поэтому использование формулы масленка для стержня, теряющего устойчивость за пределом упругости, не рекомендуется.、 Таблица 20 Материал^до Б СТ2, СТЗ…………………………………….. 100 3100H.4ST5………………………………………………… 100 4640 32.6 сталь 40………………………………………….. 90 3210 11,6 к т а л…………………………… 100 5890 38,2 чт (с О С Н а)………………………………….. 110 293 1.94 ч у г и Н………………… ………………………….. 80 7760 120 Мало того, что это в корне неправильно, но и последствия очень опасны. Поскольку теоретическое решение задачи устойчивости за пределами пропорционального предела затруднительно, обычно
используют эмпирические формулы, полученные в результате обработки Людмила Фирмаль
большого количества экспериментальных данных. Ф. С. Ясинский собрал и обработал обширный экспериментальный материал по продольному изгибу стержня, в результате чего разработал таблицу критических напряжений в зависимости от гибкости для ряда материалов.: (19.34)) Значения коэффициентов а и в некоторых материалов приведены в таблице. 20. Для использования параболической зависимости чугуна (19.35) Где с — 0,53. Согласно этим данным, 0XAG. it также можно построить график зависимости критического напряжения от гибкости стержня. В гибком значении (пусть это будет Ar) значение OCD, вычисленное по формуле (19.34) или (19.35), будет равно ОКР-А-Б% OCD=a-bh+Ca2 предельное напряжение сжатия, а именно: для пластмасс ОКР=(ТТ, Корпус
из хрупкого материала agcr= = КГК-(19.36) Стержни XAO называются стержнями с низкой гибкостью. Они рассчитывают только на силу. В этом примере (рис. 507) часть графика критических напряжений за пределами пропорциональности(4 0X 100) представляет собой слегка наклонную прямую SM, а часть (0X 40) — горизонтальную линию NS. Таким образом, граф СТЗ стали A CR= * f(X) состоит из трех частей: гиперболы Эйлера X>100, наклонной линии 40<x<100 и почти горизонтальной линии X<40=XO. Градуированная линия SM соответствует напряжению между пропорциональным пределом и пределом текучести. Горизонт SN соответствует напряжению, равному пределу текучести.
Смотрите также:

