Оглавление:





Понятие о новых теориях прочности
- Концепция новой теории прочности С точки зрения главных напряжений O1, O2, O3, инвариантных к напряженному состоянию, представлены условия перехода материала в критическое состояние и условия прочности в соответствии с различными теориями. В случае трехмерного пространства, когда координатные оси направлены в основном направлении, эти условия могут быть
выражены в виде некоторых предельных плоскостей F (O2, O3)=0. (7.22) таким образом, критическая плоскость, соответствующая условиям возникновения массового пластического деформирования согласно теории соотношения потенциальной энергии формования[см. уравнение(7.20)], (Ah-O2)2+(O2-O3)2 4-(O3-(uh) 2-2)=0(7.23)критическая плоскость (7.23) имеет ось, наклоненную равную оси цилиндра (фиг. 176, а). \у б\’ И от радиуса g=|/ -.
Для плоского напряженного состояния, когда основное напряжение равно нулю, условие(7.23) Dae ’ 1 эллиптическая предельная кривая Людмила Фирмаль
(рис. 176, б). Критерий максимального касательного напряжения соответствует критической плоскости в виде правильного шестиугольного цилиндра, вписанного в цилиндр(7.23). Критерию максимального нормального напряжения соответствует куб с ребром, равным o°. Все точки в пределах территории окружены предельной поверхностью, соответствующей напряженному состоянию, и коэффициент запаса больше. Напряженное состояние,
представленное точкой вне этой области, имеет меньший коэффициент запаса, чем это. Недостатки рассматриваемой теории и появление новых материалов послужили толчком для развития теории новой прочности. Большинство из них основано на выборе именно этой формы- Твердая поверхность, способная учитывать свойства сопротивления материалов этого класса в сложном напряженном состоянии. Рассмотрим несколько новых теорий.
- Ю. И. Яги предложил принять критическую плоскость (7.22) в качестве полинома второго порядка к третичному напряжению: («1—»g) 2+(O2—»z) g+(°z—»i) 2+a (<*i+A2+O3) 2++B (o,+A2+O3)=C, (7.24) это изотропное уравнение изотропно. Определите формулу для константы, установив допустимые напряжения[I], [o__] и [t]при растяжении, сжатии и сдвиге соответственно: 6 [т]2-2[о](о]Т6 [Т] 2([о]-м) a=»- — — — — FTKj——— ; —— []- — — — — ’ S=6 м2- Из вышесказанного ясно, что теория Ю. И. Ягна позволяет учитывать неравномерное сопротивление материала растяжению и сжатию, а также сопротивление материала сдвигу. При специфическом соотношении между введенными константами a, b и C формула (7.24) содержит
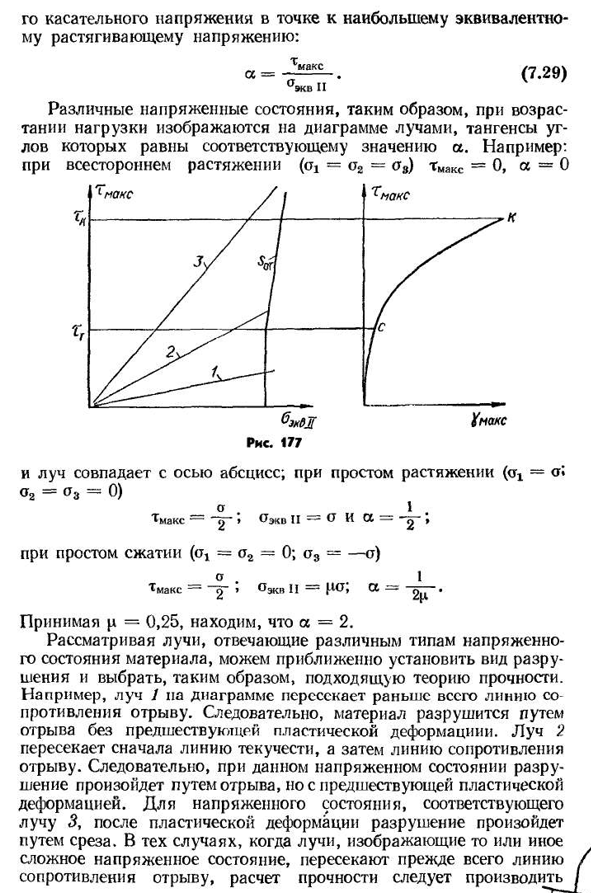
несколько энергетических критериев, в том числе критерии удельной потенциальной энергии изменения формы.) Г. С. Писаренко и А. А. Лебедев считают, что наступление предельного состояния обусловлено способностью материала противостоять как тангенциальным, так и нормальным напряжениям, а также функцией тангенциального напряжения и напряженного состояния, например, предложен следующий критерий линейной формы: Токт+Т2. (7.25)выражение TOC дается выражением (6.25). Константы/Гц и Tg материала могут быть выражены в терминах предельного напряжения o°>oL при одноосном растяжении и сжатии. Тогда условие (7.25) принимает вид-D-Htoct+(1-X) O1 ’ ®Oeecqvvvv I1I1 — RRSSHT, CCtt —- Предполагая P=0.25, вы можете видеть, что это OS=2. Рассматривая световой пучок, соответствующий
напряженному состоянию различных типов материалов, мы можем Людмила Фирмаль
аппроксимировать тип разрушения и, следовательно, выбрать соответствующую теорию прочности. Например, Луч 1 на рисунке сначала пересекает линию сопротивления изоляции. В результате материал разрушается путем разделения без предварительной пластической деформации. Луч 2 сначала пересекает линию текучести, а затем линию сопротивления разрыву. Поэтому в заранее определенном напряженном состоянии разрушение происходит путем отслаивания, но вызвано предшествующей пластической деформацией. Из-за условия давления, соответствующего балке 3, после пластической деформации трещина делается путем сдвига. Если балка, представляющая то или иное сложное напряженное
состояние, сначала пересекает линию сопротивления отрыву, то необходимо выполнить прочностные расчеты 7 8-2770po теория моля, вторая или Первая теория прочности. Если балка сначала пересекает линию предела текучести, то расчет прочности следует проводить в соответствии с третьей или четвертой теорией прочности. Таким образом, диаграммы механических состояний с известным приближением отражают зависимость формы разрушения от типа напряженного состояния. Конструктивное приближение состоит в том, что предел текучести и трещиностойкость нестабильны. Лучи, представляющие напряженное состояние, являются прямыми только до тех пор, пока они не достигнут предела текучести.
Смотрите также:
| Задачи теорий прочности | Примеры проверки прочности |
| Классические критерии прочности (теории прочности) | Сдвиг. расчет на срез |

